MATLAB神器！轻松求解线性方程组App，一试即会！

基于MATLAB求解线性方程组的App详解

一、引言：线性方程组的魅力与挑战

线性方程组，作为数学领域的一颗璀璨明珠，广泛应用于工程、经济、物理等多个领域。它以其简洁的形式和深刻的内涵，吸引着无数数学爱好者和专业人士去探索其奥秘。求解线性方程组并非易事，尤其是当方程组的规模较大、变量较多时，手动求解几乎成为不可能的任务。

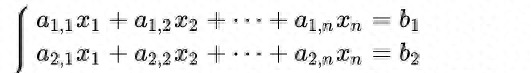
幸运的是，随着计算机技术的发展，我们可以借助MATLAB等强大的数学软件来求解线性方程组。MATLAB不仅提供了丰富的数学函数和工具箱，还允许用户通过编写程序来定制自己的求解工具。本文将介绍一个基于MATLAB的线性方程组求解App，帮助读者快速、准确地求解各种形式的线性方程组。

二、线性方程组的解的情况：深入剖析与实例展示

在深入探讨基于MATLAB的线性方程组求解App之前，我们有必要先了解一下线性方程组的解的情况。线性方程组的解取决于其系数矩阵和增广矩阵的秩，以及未知数的个数。根据不同的条件，线性方程组可能有无解、唯一解或无穷多解。

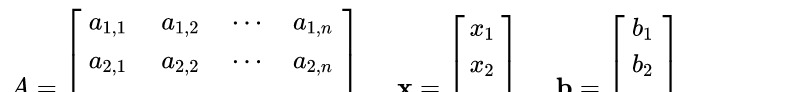
以齐次线性方程组为例，当系数矩阵的秩等于未知数的个数时，方程组只有零解；当系数矩阵的秩小于未知数的个数时，方程组有无穷多解，且这些解构成一个线性空间。非齐次线性方程组的情况则更为复杂，需要根据系数矩阵和增广矩阵的秩的关系来判断方程组是否有解以及解的个数。

为了更直观地展示线性方程组的解的情况，我们可以结合一些具体的实例来进行说明。比如，我们可以构造一个3x3的齐次线性方程组，通过计算其系数矩阵的秩来判断方程组的解的情况。同样地，我们也可以构造一个非齐次线性方程组，并通过比较系数矩阵和增广矩阵的秩来确定方程组的解。

三、基于MATLAB的线性方程组求解App：操作便捷，功能强大

接下来，我们将重点介绍基于MATLAB的线性方程组求解App。这款App具有操作便捷、功能强大的特点，能够帮助用户快速求解各种形式的线性方程组。

我们来看一下App的安装步骤。用户只需下载压缩包并解压，然后在MATLAB中双击安装文件即可。安装过程简单明了，无需复杂的配置和设置。

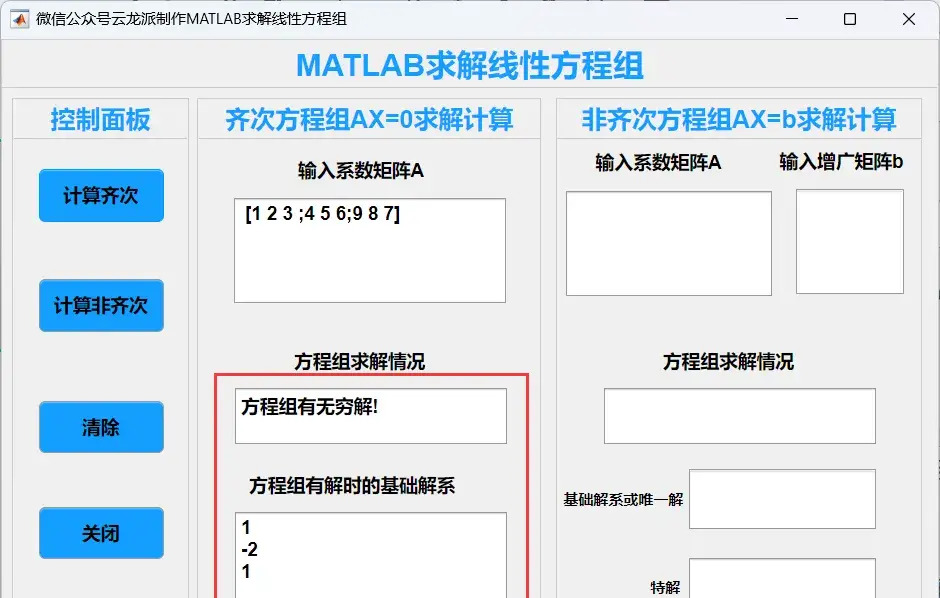
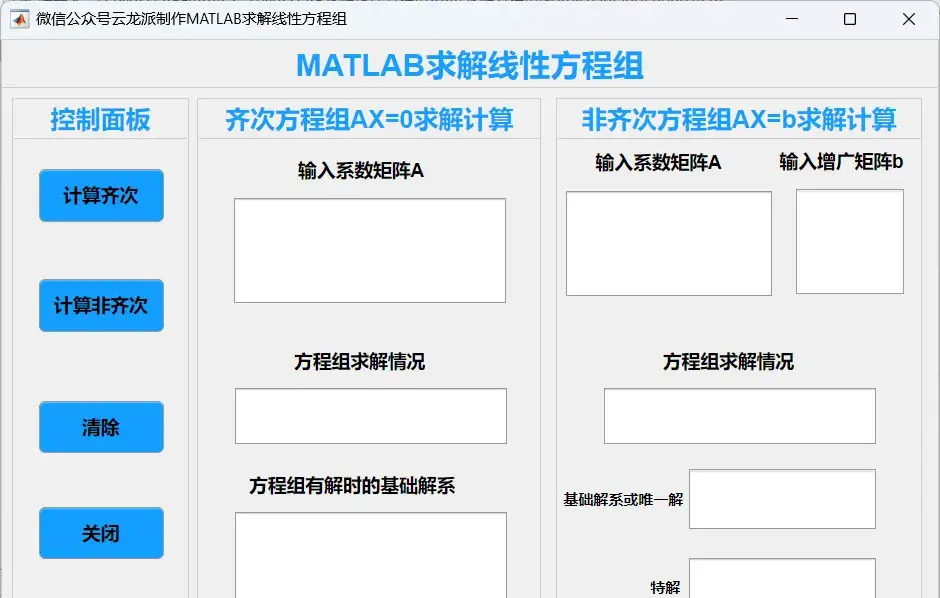
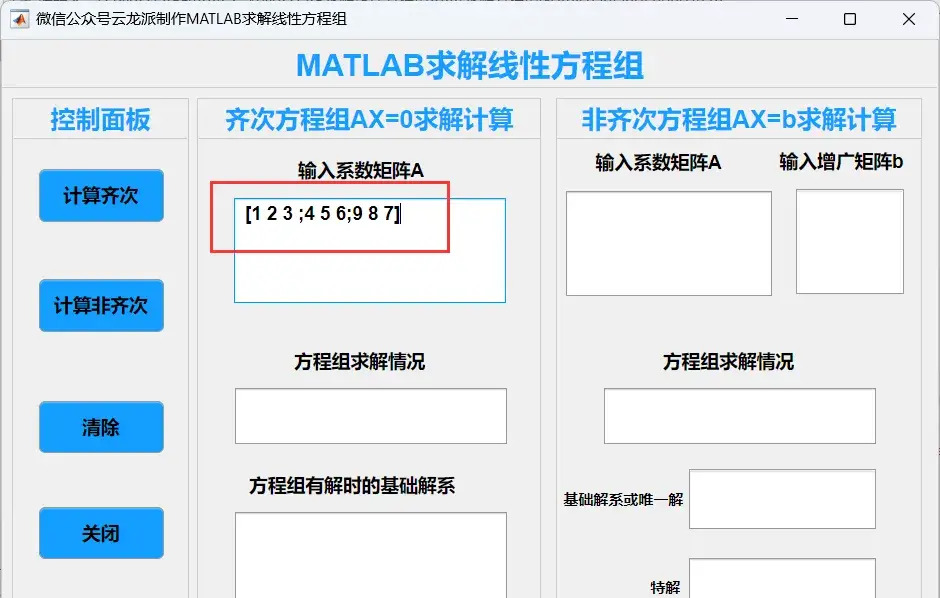
安装完成后，我们就可以开始使用这款App了。我们需要输入齐次线性方程组的系数矩阵。App提供了友好的界面和清晰的输入框，方便用户输入数据。接下来，点击计算齐次按键，App就会根据输入的系数矩阵判断方程组的解的情况，并计算出基础解系（如果有解的话）。

对于非齐次线性方程组，我们需要输入系数矩阵和增广矩阵。同样地，App会根据输入的数据判断方程组的解的情况，并计算出基础解系和特解（如果有解的话）。如果方程组有唯一解，App还会直接给出这个唯一解。

除了基本的求解功能外，这款App还提供了一些额外的功能。比如，用户可以通过清除按键清除输入的数据，以便进行下一次计算。App还提供了关闭按钮，方便用户随时退出程序。

四、App编程实现与核心技术

这款基于MATLAB的线性方程组求解App的实现离不开MATLAB强大的编程环境和丰富的数学库。在编程实现过程中，我们主要利用了MATLAB的矩阵运算功能和线性代数工具箱。通过编写简洁明了的代码，我们实现了方程组的输入、计算、结果展示等功能。

在核心技术方面，我们采用了高斯消元法来求解线性方程组。高斯消元法是一种经典的线性方程组求解方法，它通过一系列的行变换将系数矩阵转化为上三角矩阵或对角矩阵，从而求出方程组的解。这种方法具有广泛的应用范围和较高的计算精度，能够满足大多数实际问题的需求。

五、实际应用案例与效果展示

为了验证这款App的实用性和有效性，我们进行了一系列实际应用案例的测试。这些案例涵盖了不同规模、不同形式的线性方程组，包括齐次线性方程组和非齐次线性方程组。

在测试过程中，我们发现这款App能够准确、快速地求解各种线性方程组，并给出清晰的结果展示。无论是系数矩阵的规模较大还是方程组的形式较复杂，App都能够轻松应对，展现出强大的计算能力和稳定性。

我们还收集了一些用户的使用反馈。大多数用户表示，这款App操作简便、功能强大，能够大大提高他们求解线性方程组的效率。一些用户还提出了一些改进建议，比如增加方程组的可视化展示功能、优化输入数据的校验机制等。这些建议为我们进一步完善App提供了宝贵的参考。

六、结语：技术之美，在于实用与高效

通过以上对基于MATLAB的线性方程组求解App的详细介绍和实际应用案例的展示，我们可以看到技术之美不仅在于其深邃的理论和精妙的算法，更在于其能够解决实际问题并带来实际效益。

这款App正是技术与实用相结合的典范。它利用MATLAB强大的编程环境和数学库，实现了线性方程组的快速求解和结果展示。它还注重用户体验和操作