素性检验新突破：区间分段筛技术揭秘！

素性检验之区间分段筛：探寻素数的高效之道

在数字的世界里，素数就像一颗颗璀璨的星辰，点缀在数学的夜空中。素数，只有两个正因数：1和它本身的自然数。它们在密码学、数据加密、算法设计等领域有着广泛的应用。今天，我们就来探讨一种高效的素数筛选方法——区间分段筛（Segmented Sieve）。

一、初识分段筛

区间分段筛，顾名思义，是将一个大的筛选范围分割成若干个小区间，然后对每个小区间分别进行筛选。这种方法在处理大数据集时特别有效，因为它能够显著降低内存消耗，并提高筛选效率。与传统的埃拉托斯特尼筛法（Sieve of Eratosthenes）相比，分段筛更加灵活，特别适用于在有限资源环境下寻找大素数。

二、分段筛的原理

分段筛的基本原理是将整个筛选范围划分为多个小区间，然后对每个小区间进行独立的筛选操作。这样做的好处是，我们不需要一次性为整个范围分配内存，从而节省了空间。由于每个小区间的筛选可以独立进行，这也为并行处理提供了可能，进一步提高了筛选效率。

在筛选过程中，我们首先需要确定一个“基准”素数列表，这些素数通常小于或等于筛选范围的平方根。然后，我们利用这些基准素数去筛选每个小区间内的数。通过不断排除合数，我们最终能够得到该区间内的所有素数。

三、时间复杂度和空间复杂度

在讨论分段筛时，我们不得不提及其时间复杂度和空间复杂度。时间复杂度反映了算法执行所需的时间，而空间复杂度则体现了算法对内存的需求。分段筛通过优化内存使用和提高并行处理能力，在这两个方面都表现出了显著的优势。

具体来说，分段筛的时间复杂度通常低于传统的埃拉托斯特尼筛法，尤其是在处理大数据集时。由于分段筛采用分而治之的策略，其空间复杂度也得到了有效控制。这使得分段筛成为处理大规模素数筛选问题的理想选择。

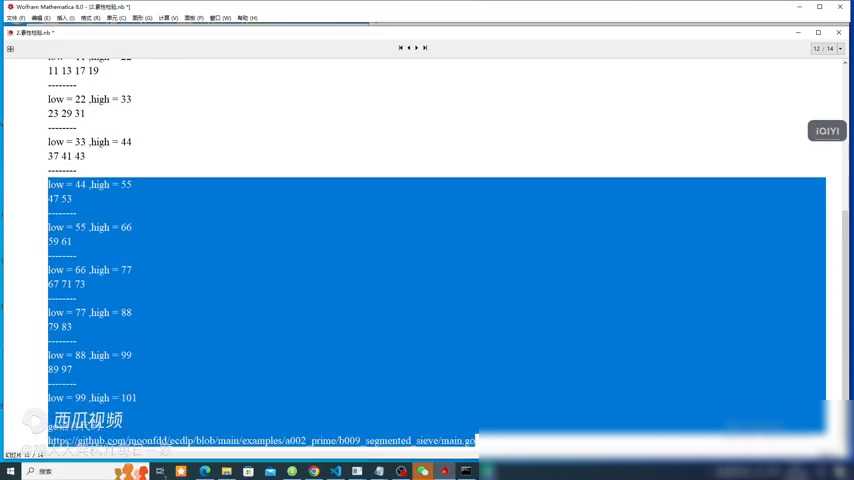
四、实例讲解：探寻47到101之间的素数

为了更直观地理解分段筛的工作原理，让我们通过一个具体实例来讲解。假设我们要在47到101的范围内寻找素数。

我们计算这个范围的上限的平方根，即√101，得到的结果大约是10.05。由于我们只需要小于这个值的素数作为筛选基准，因此我们可以确定基准素数列表为：2, 3, 5, 7。

接下来，我们从47开始筛选。由于47本身就是一个素数（它大于任何一个基准素数且不能被它们整除），我们将其记录下来。然后，我们继续检查48、49、50等后续的数，直到101。在这个过程中，我们不断利用基准素数列表来排除合数。

最终，我们得到的素数列表包括：47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 和97。注意，虽然101在我们的筛选范围内，但由于我们已经达到了筛选的上限，所以在这个特定的例子中并没有将其包括在内（在实际应用中，我们通常会根据具体情况调整筛选范围以确保不遗漏任何素数）。

五、分段筛的应用与优势

分段筛作为一种高效的素数筛选方法，在多个领域都有着广泛的应用。在密码学中，素数被广泛用于生成公钥和私钥对；在数据加密中，大素数的难以预测性为数据的安全性提供了有力保障；在算法设计中，素数也扮演着重要角色，如哈希函数的设计等。

分段筛的优势在于其灵活性和高效性。通过将筛选范围划分为多个小区间并独立处理，分段筛不仅降低了内存消耗，还为并行处理提供了可能。这使得分段筛在处理大规模数据时具有显著优势。

六、结语

素数作为数学的基础元素之一，其重要性不言而喻。分段筛作为一种高效的素数筛选方法，为我们提供了一种在有限资源环境下快速寻找大素数的有效途径。通过本文的介绍，希望读者能够对分段筛有更深入的了解，并能够在实际工作中加以应用。