描述性统计：如何精准分析数据集中趋势与分散性？

描述性统计：如何精准分析数据集中趋势与分散性？

亲爱的读者朋友们，今天我们来聊一个与我们日常工作和生活息息相关的话题——描述性统计。它帮助我们更好地理解和分析数据，从而在做出重要决策时能够更有把握。那么，如何深入掌握位置度量与离散度度量这两个关键指针呢？接下来，我们将逐一解析这两个领域的核心内容与实际应用。

一、描述性统计的重要性

描述性统计是数据分析领域的一项基本技能，它帮助我们对数据进行概括和总结。在做研究、撰写报告，乃至日常工作中，掌握描述性统计不仅能提供清晰的数据视图，还能够为进一步的分析打基础。通过监测关键指标，如销售额、用户增长、产品质量，企业可以及时调整战略和策略。

描述性统计分为两大类：位置度量与离散度度量。位置度量揭示数据的中心位置，而离散度度量则帮助我们了解数据的变异性。这两者相辅相成，构成了数据分析的基本框架。

二、描述性统计概述

2.1 位置度量的定义

位置度量是描述数据分布集中趋势的指标。它表征了数据的“中心”，反映了我们可以期待的数值。在很多业务场景中，位置度量能够直接影响决策，比如在客户满意度调查中，平均分和中位数可能呈现出完全不同的结果。因此，了解和掌握位置度量的计算方法非常重要。

在实际应用中，使用位置度量来分析数据时，首先要确保数据的整洁性和完整性。去除异常值与错误数据后，再进行计算。常用的位置度量方法包括算术平均数、中位数和众数，各有其特定的应用场景。

2.2 离散度度量的定义

与位置度量互为补充的，则是离散度度量。离散度度量反映了数据的分散程度，有助于我们判断数据的稳定性及一致性。假设有多个产品的销售数据，离散度越高，说明各个产品的销售表现差异越大，意味着市场需求不均衡。

常见的离散度度量指标包括极差、分位数、方差和标准差。在分析数据时，离散度的掌握不仅可以帮助我们识别根本问题，还可以引导我们制定相应的维护和改进措施。

三、位置度量指标

3.1 算术平均数

算术平均数是最常见的位置度量，通常用对称的方式来理解。其计算方法简单，即将所有观测值求和后除以观测值的数量。例如，一家养殖公司管理六个猪站，2021年6月生产了整整22000袋猪精产品。若我们求得平均数，结果是3666.67袋。

在企业管理中，算术平均数可以帮助决策者快速评估整体表现。然而，算术平均数的计算也存在一定的局限性。例如，当存在极端值时，算术平均数可能会失去代表性。假设某个猪站由于特殊情况，生产了30000袋猪精产品，重新计算的平均数将会大幅度提升，使得整体评估呈现偏差。

提高算术平均数的实用性有以下几点建议：

- 定期审核数据，确保其准确性；

- 在数据集中强烈偏向极值时，考虑使用其他位置度量。

3.2 中位数

中位数是另一种重要的位置度量，代表数据集中的中间值。它的一个显著优点是抗极端值。例如，在一组公猪的月龄数据中，若我们有23、23、24、28、30、40、43和48月龄，那么计算得到的中位数就是30月龄。

在很多实际场景中，中位数的使用更加稳健。经济学家通常用中位数收入来评估一个地区的经济水平，因为它能有效避免因少数富人收入过高而导致的误导。要计算中位数，尤其需注意：

- 数据必须进行排序；

- 奇数和偶数样本的中位数计算略有不同，确保方法准确。

3.3 众数

众数是样本中频率最高的观测值，适合用于分类数据分析。例如，若我们有一组公猪月龄为23、23、24、28、28、28、30、40、43和44月龄，那么28便是众数。

众数在数据分析中的价值在于它的适用范围广，可以用来明确市场需求或客户偏好。比如，在电商行业，众数可以帮助商家明确消费者选择的热门产品，从而优化库存。对众数的注意事项包括：

- 变量可能有多个众数；

- 在偏态分布的数据中，众数与其他定位量的关系需要谨慎对待。

四、离散度度量指标

4.1 极差

极差是离散度度量中的最简单指标，它通过计算数据集中的最大值与最小值之间的差距来衡量数据的分散程度。例如，如果一个产品在一个月内的销量分别为100、150、200和300，那么它的极差就是300 - 100 = 200。

极差虽然简单易懂，但它的局限性在于容易受极端值影响。为了提高分析精度，可以借助其他离散度度量指标来增强判断力。

4.2 百分位数

百分位数，顾名思义，表示某个数据值在数据集中所处的相对位置。利用百分位数，我们可以清晰地了解个体在整体中的相对位置。例如，一组数据经过排序后，若第25百分位数（Q1）是15，则说明在这组数据中，25%的数据值小于或等于15。

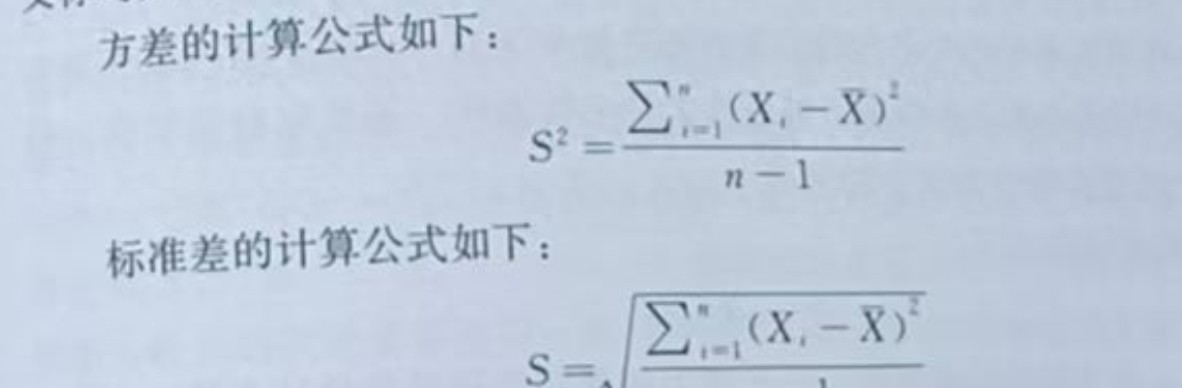
四分位数也是常用的一种表现方式，它将一组数据分割为四等份，能直观展示数据的分布状态。分析数据时，可以通过以下方式获取有意义的信息：

- 较低的Q1与较高的Q3之间的差值可以反映出数据的离散程度；

- 可视化工具（如箱形图）能直观展示四分位数信息。

4.3 方差与标准差

方差和标准差是衡量数据变异性的两大重要指标。方差表示每个观测值与算术平均数之间的离差平方和的平均值，而标准差则是方差的平方根。通过这两个指标，我们可以更全面地了解数据的分散情况。

从实际操作的角度来看，如果我们以数据1、2、3、4、5、6为例，其平均值为3.5。可以通过计算方差得到3.5，再进一步算出标准差为1.87。方差与标准差的意义在于，它们能够帮助我们判断一个数据集的波动性。例如，若多个样本的标准差偏高，管理层需要注意可能存在的运营风险。

在使用方差和标准差时，务必记得：

- 数据的正态分布形式常常可以用于估算标准差；

- 在对比不同数据集时，需确保它们的数据单位和数量一致。

完整理解这两个指标，可以更有效地指导企业决策。

通过对位置度量与离散度度量的详细解析，我们不仅能够更好地理解数据背后的规律，还能够将之应用于实际工作中，提升决策的科学性及有效性。
欢迎大家在下方留言讨论，分享您的看法！