高阶函数揭秘！逻辑斯谛模型捕捉非线性生长！

高阶函数模型：捕捉非线性生长模式的逻辑斯谛

一、引言

在自然界和许多其他复杂系统中，增长并非总是线性的。比如，生物种群在有限的资源环境中，其增长模式往往是非线性的。为了更准确地描述这种增长，高阶函数模型应运而生，其中的佼佼者就是逻辑斯谛增长模型。这个模型不仅帮助我们理解生物种群的增长动态，还在经济学、人口学等多个领域有着广泛的应用。

二、高阶函数模型与逻辑斯谛增长模型

1. 高阶函数模型：不仅仅是线性关系

高阶函数模型，顾名思义，就是函数中包含了高阶项，这使得模型能够描述更为复杂的非线性关系。在现实世界中，很多现象并非简单的线性关系所能刻画，比如生物种群的增长。当资源有限时，种群的增长速度会随着数量的增加而减缓，这就是典型的非线性关系。高阶函数模型正是为了捕捉这种关系而诞生的。

2. 逻辑斯谛增长模型：模拟有限资源下的生物增长

逻辑斯谛增长模型是一种特殊的高阶函数模型，它特别适用于描述在有限资源环境下的生物种群增长。这个模型的关键在于，它假设种群的增长率与当前种群数量之间存在一种非线性关系。换句话说，随着种群数量的增加，每个个体所能获取的资源减少，从而导致增长率下降。

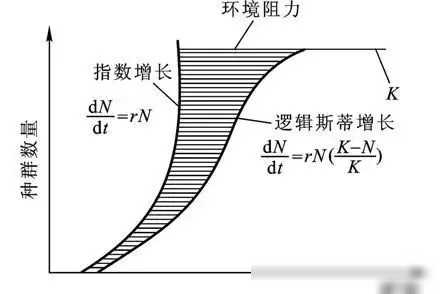
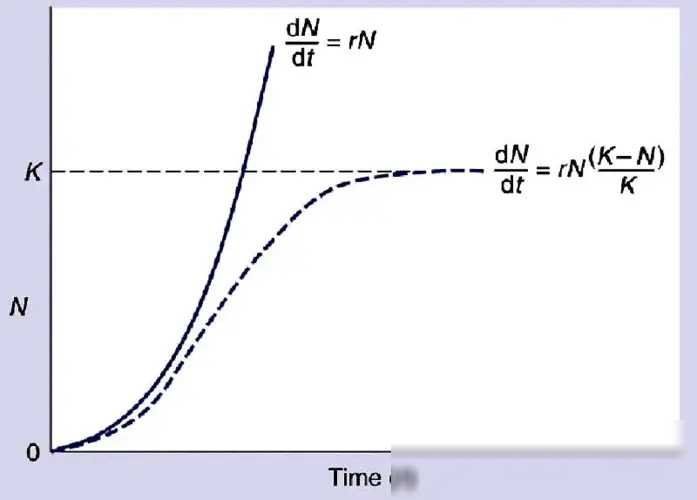
逻辑斯谛增长模型的数学表达式通常是这样的形式：dN/dt = rN(1 - N/K)，其中N是种群数量，t是时间，r是种群的内禀增长率，K是环境容纳量。这个模型通过引入非线性项(1 - N/K)，成功地刻画了种群增长过程中的资源限制效应。

三、逻辑斯谛增长模型的应用

1. 生态学：预测物种的最大种群数量

在生态学中，逻辑斯谛增长模型被广泛用于预测物种在特定环境下的最大种群数量。通过拟合模型参数，我们可以估算出物种的增长率和环境容纳量，从而预测种群数量的动态变化。这对于保护濒危物种、管理自然资源具有重要意义。

例如，假设我们有一个濒危物种的种群数量数据，我们可以使用逻辑斯谛增长模型来拟合这些数据，并预测该物种在未来几年内的种群数量。这样，保护机构就可以根据预测结果制定相应的保护措施。

2. 经济学：模拟商品销售增长

在经济学领域，逻辑斯谛增长模型同样有其应用价值。想象一下，一个新产品刚上市时，销售量可能会迅速增长。但随着市场逐渐饱和，销售增长速度会放缓。这个过程与生物种群的增长非常相似，因此逻辑斯谛增长模型可以很好地模拟这种销售增长模式。

比如，某款新型智能手机上市后的销售数据可能呈现出逻辑斯谛增长的趋势。初期，由于产品新颖且市场需求大，销售量快速增长。但随着时间的推移，市场逐渐饱和，销售增长速度开始放缓。通过使用逻辑斯谛增长模型，企业可以预测未来的销售趋势，从而制定更加精准的市场策略。

3. 人口学：预测人口增长趋势

在人口学领域，逻辑斯谛增长模型也被广泛用于预测人口增长趋势。考虑到资源、环境等因素的限制，人口的增长往往也呈现出非线性的特点。通过使用逻辑斯谛增长模型，我们可以更加准确地预测未来的人口数量，为政策制定者提供有价值的参考信息。

以某个国家的人口数据为例，我们可以使用逻辑斯谛增长模型来拟合历史人口数据，并预测未来的人口增长趋势。这样，政府就可以根据预测结果来制定相应的人口政策、教育政策等，以应对未来可能出现的人口问题。

四、高阶函数模型的局限性与优化

虽然高阶函数模型如逻辑斯谛增长模型在捕捉非线性生长模式方面具有显著优势，但它们也并非万能。每个模型都有其适用范围和局限性。例如，逻辑斯谛增长模型假设种群增长率是随着种群数量的增加而逐渐减小的，这在某些情况下可能并不成立。此外，模型中的参数估计也可能受到数据质量和数量的影响。

为了优化模型的准确性和可靠性，我们可以采取多种措施。我们需要根据实际情况选择最合适的模型类型。我们可以通过收集更多、更准确的数据来提高参数估计的精度。我们还可以考虑引入其他影响因素来完善模型，比如考虑环境变化、人为干扰等因素对种群增长的影响。

五、总结与展望

高阶函数模型如逻辑斯谛增长模型为我们提供了一种强大的工具来捕捉和模拟非线性生长模式。这些模型在生态学、经济学和人口学等多个领域都有着广泛的应用价值。我们也要认识到每个模型的局限性和适用范围。通过不断优化模型和提高数据质量，我们可以更好地利用这些工具来揭示自然界的奥秘并服务于人类社会。

展望未来，随着科技的进步和研究的深入，我们相信高阶函数模型将在更多领域发挥重要作用。例如，在人工智能领域，这些模型可能用于预测机器学习算法的性能；在生物医学领域，它们可能用于模拟疾病的传播过程；在环境科学领域，它们可能用于评估气候变化对生态系统的影响等等。让我们拭目以待这些模型在未来的精彩表现吧！