排序算法揭秘:冒泡排序与选择排序的完美较量,你选谁?
排序算法揭秘:冒泡排序与选择排序的完美较量,你选谁?
亲爱的读者朋友们,今天,我们来聊聊计算机中至关重要的两个排序算法——冒泡排序和选择排序。它们不仅是编程入门的“必修课”,而且在数据处理和优化算法的过程中扮演着关键角色。那么,它们到底有什么特点?适用什么场景?接下来,跟我一起深入探讨吧!
一、排序的重要性
今天的数据世界中,排序是一项不可或缺的操作。无论是在数据库管理、电子商务推荐系统,还是在大数据分析,数据的排序都能显著提升检索和处理的效率。比如,在电商平台上,当用户筛选商品时,后台数据库会根据价格、销量等进行排序,以便用户快速找到符合需求的产品。

在技术层面,排序能够帮助我们在查找、合并数据时节省大量的时间。假设你设计了一款求职招聘应用,其中求职者的简历是按时间先后排列的,这时候使用排序算法,将简历从最新到最旧排列,可以帮助招聘人员轻松找到最能引起注意的申请者。排序在数据结构中提升了查询速度,提高了系统的整体性能,是我们在编程时首先要掌握的技能。
二、冒泡排序
1. 冒泡排序的原理
冒泡排序(Bubble Sort)是一种经典的排序算法,其基本思想就是不断比较相邻两个元素的大小,将较大的元素“冒泡”到最后。
举个简单例子,假设你有一组数据 [5, 3, 8, 4, 2],在第一轮比较中,首先比较5与3,5较大,于是将它们交换;接着比较5与8,5较小,不交换;然后比较8与4,8较大,交换位置。经过一轮比较后,最大的元素8已经“冒泡”到了末端。这一过程重复进行,直到整个数组有序。显然,冒泡排序的时间复杂度为O(n^2),适合小规模数据排序。
2. 冒泡排序的特点
冒泡排序的最大特点在于它的稳定性和易实现性。在排序过程中,如果两个元素相等,它们的相对位置不变。此外,冒泡排序可以通过设置一个标志位来优化操作——若在某次遍历中没有发生交换,说明数据已经有序,可以提前结束排序。
需要注意的是,由于冒泡排序的时间复杂度较高,所以在处理大规模数据时并不高效。根据统计,冒泡排序在处理1000条数据时可能需要进行近500,000次比较,而快速排序在处理相同数量的数据时,仅需约13,000次。
3. 冒泡排序的实现
在实际编程中,我们通常在语言的选择上能够随意搭配。以下是一个用Java编写的简易冒泡排序代码示例:
```java
public class BubbleSort {
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
// 交换位置
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
}
```
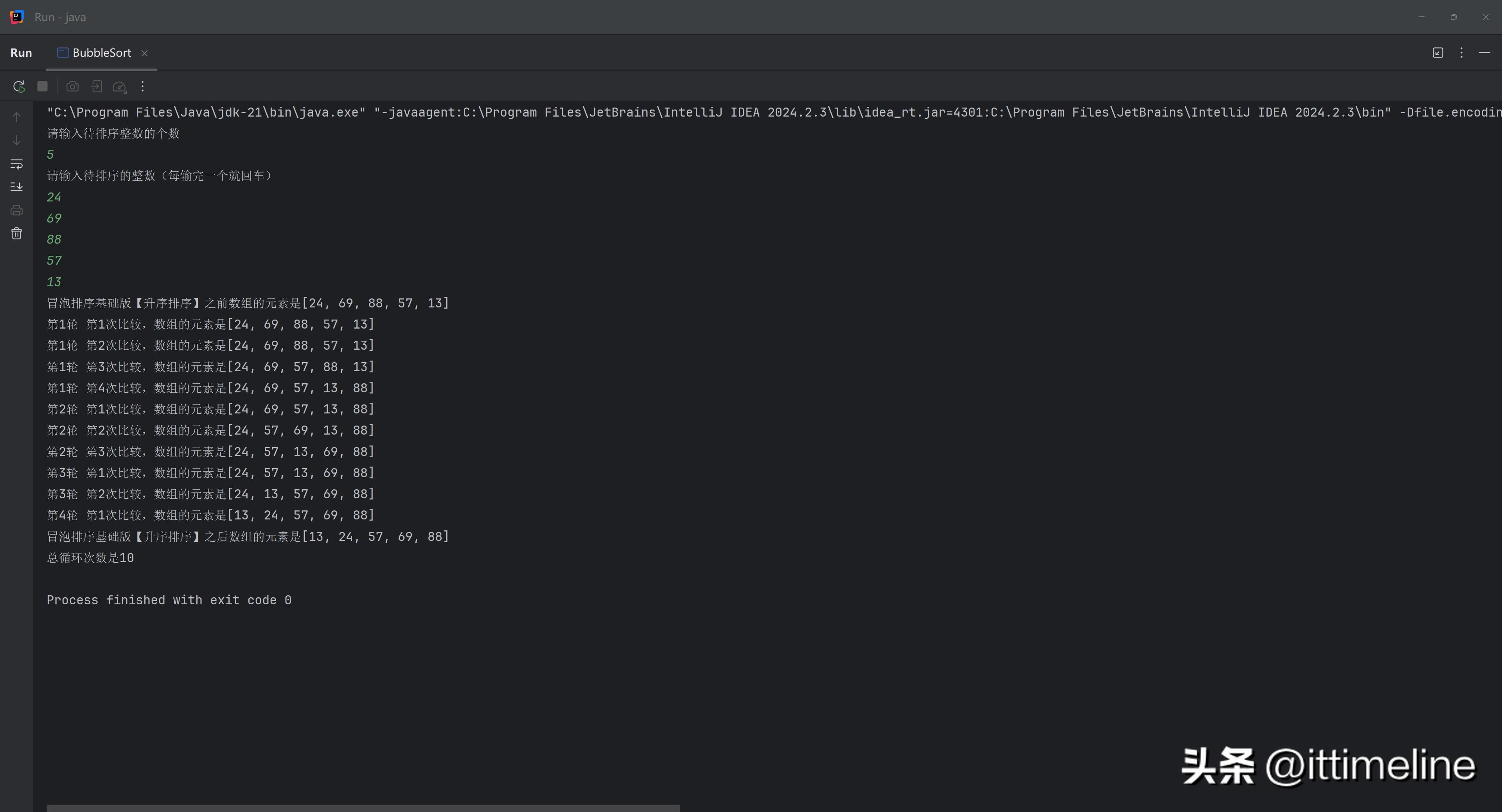
运行这段代码,你会得到一个有序的数组。这里的核心是两重循环,外层循环控制轮次,内层循环进行元素比较与交换,结构清晰,易于理解。
4. 冒泡排序的优化
虽然冒泡排序看上去简单易懂,但其效率确实不够高。因此,程序员们常常研发出各种优化算法。在此,我们可以对冒泡排序进行优化,通过标志位来减少不必要的遍历:
```java
public class OptimizedBubbleSort {
public static void optimizedBubbleSort(int[] arr) {
int n = arr.length;
boolean swapped;
for (int i = 0; i < n - 1; i++) {
swapped = false; // 重置标志位
for (int j = 0; j < n - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
// 交换位置
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true; // 标志位设置为true
}
}
// 如果没有交换,提前退出
if (!swapped) {

break;
}
}
}
}
```
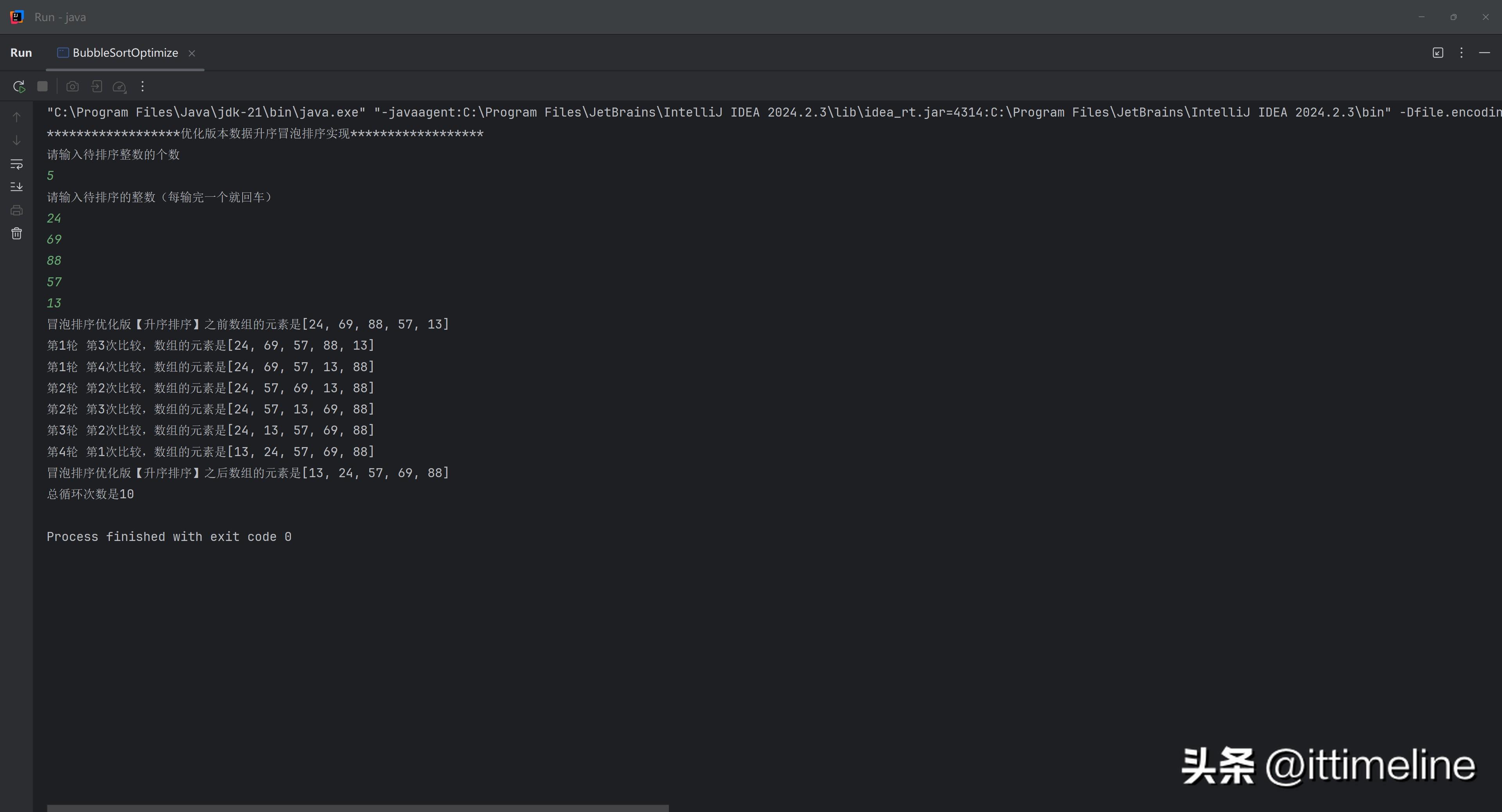
要点在于一旦数组已经有序,不再进行多余的遍历,极大地提高了效率。通过这种小技巧,在最优情况下,我们甚至可以达到O(n)的时间复杂度,非常值得在实际编程中尝试。
三、选择排序
1. 选择排序的基本思想
选择排序(Selection Sort)是一种相对简单的比较排序算法。它的核心思想是找到未排序部分的最小(或最大)元素,将其放到已排序序列的末尾。可以想象成老师在批改试卷,先找到分数最低的,然后将他移到已排名的位置,再继续处理剩余试卷。
对于数组 [5, 3, 8, 4, 2],在第一轮比较中,找到2并将其放到最前面,接着找到3并放到第二个位置,依此类推,直到所有元素有序。选择排序的时间复杂度同样是O(n^2),但由于每轮只进行一次交换,这使得它相对冒泡排序在交换次数上较少,更适合大规模数据的有序处理。
2. 选择排序的实现
实现选择排序非常简单,以下是Java代码示例:
```java
public class SelectionSort {
public static void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i; // 假设当前元素为最小元素
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j; // 更新最小元素的索引
}
}
// 交换最小元素和当前元素
if (minIndex != i) {
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
}
}
```
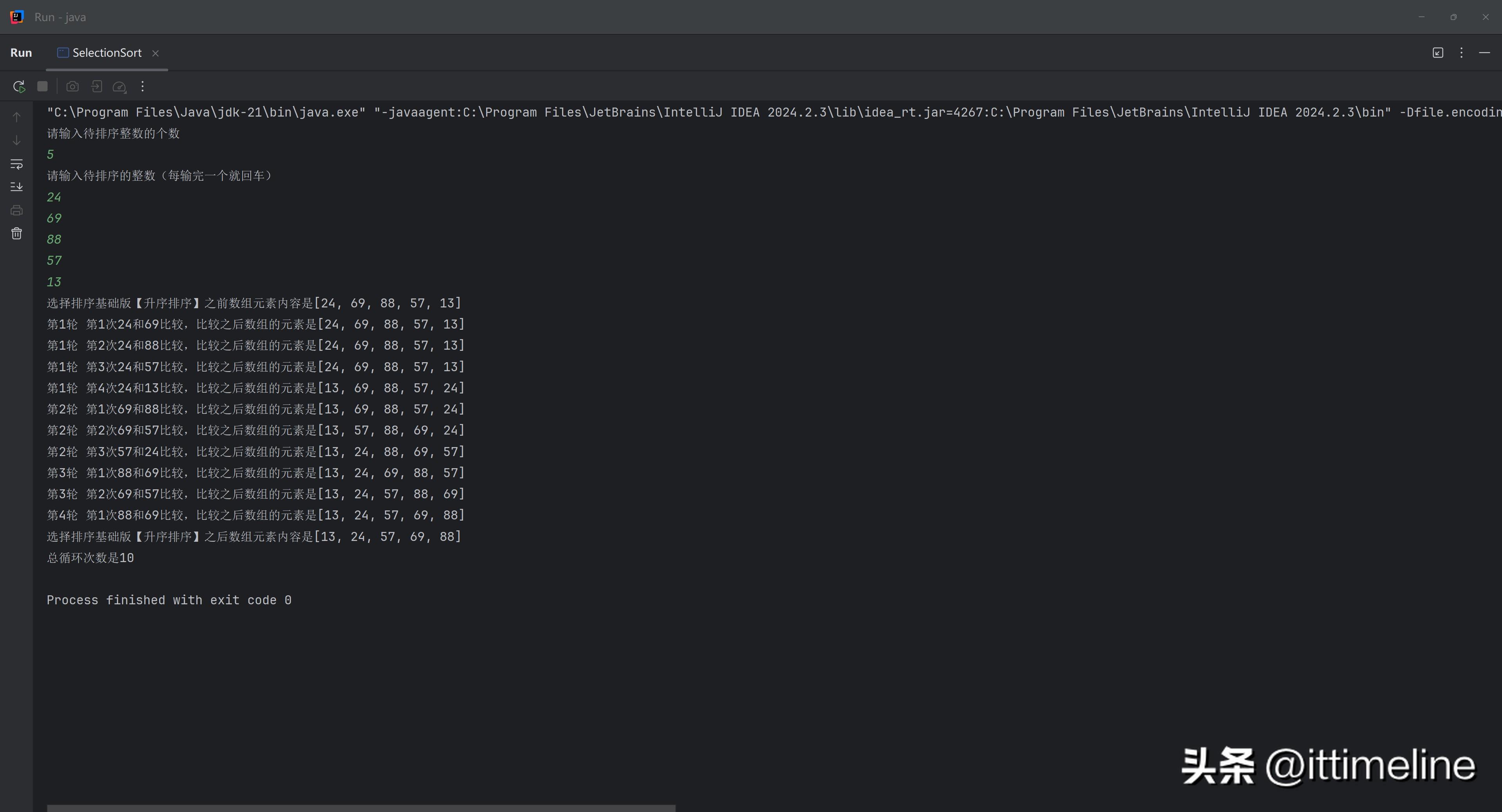
从代码中我们可以看出,选择排序的实现过程相对直观,通过找到最小值的索引并交换位置,整个过程简单易懂易于调试。
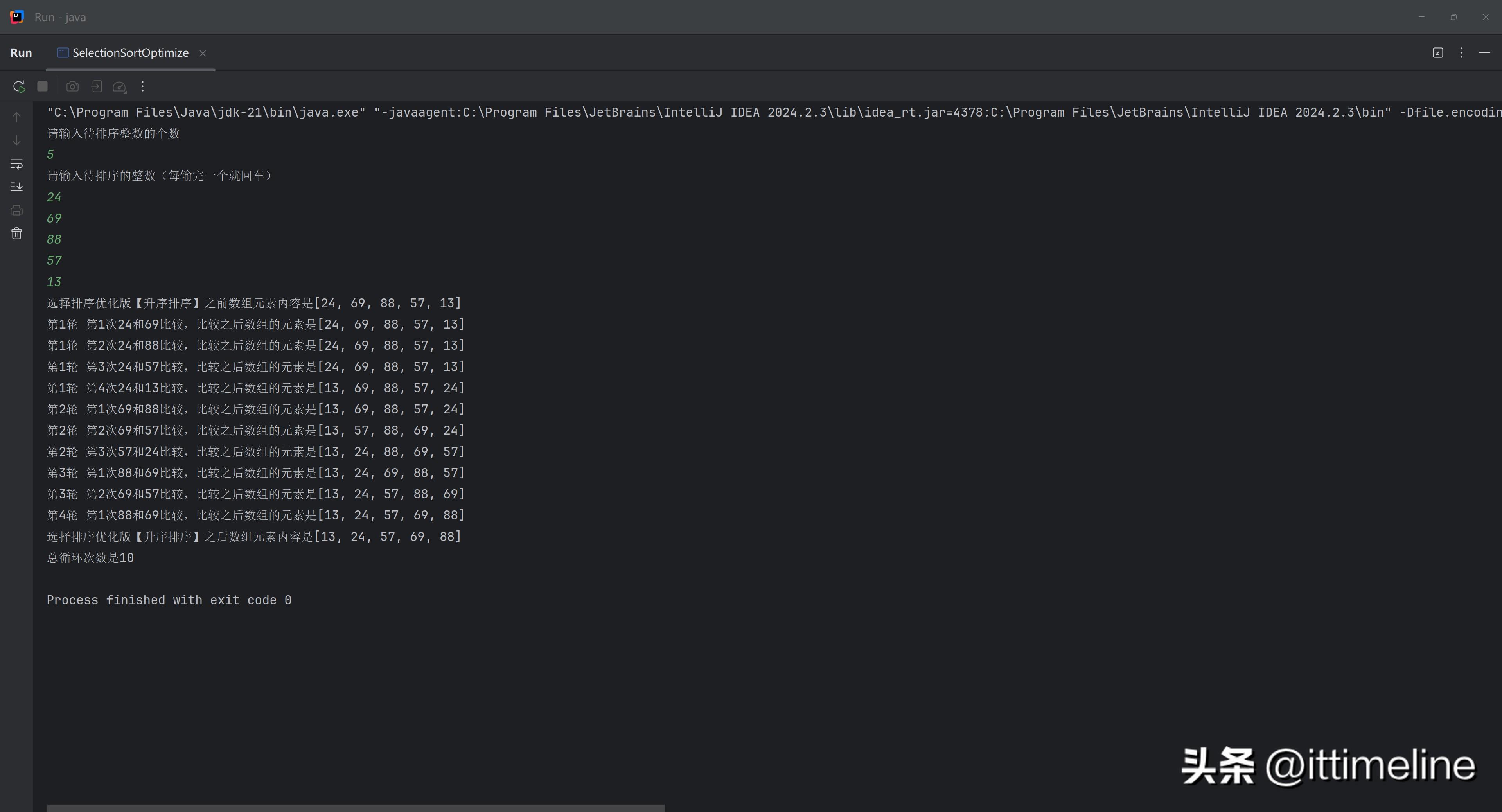
3. 选择排序的优化
针对选择排序的优化,虽然选择排序的本质没有改变,但可以通过缓存已排序部分来进一步降低时间复杂度。在许多情况下,为了提升性能,程序员们会将选择排序与其它排序算法结合进行排序,形成 hybrid(混合)算法。例如,在处理小规模数据时,可以使用插入排序配合选择排序,实现更高效的排序过程。以下是简化版的实现:
```java
public class HybridSort {
private static final int INSERTION_SORT_THRESHOLD = 10;
public static void hybridSort(int[] arr) {
if (arr.length < INSERTION_SORT_THRESHOLD) {
insertionSort(arr);
} else {
selectionSort(arr);
}
}
private static void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
// 将大于key的元素移动到前面
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
private static void selectionSort(int[] arr) {
// 同上
}
}
```
通过这种方式,混合算法能有效提升整个排序过程的效率,特别是当数据规模较小的情况下,效果尤为明显。
四、冒泡排序与选择排序的优缺点对比
在比较这两种排序算法的优缺点时,需要考虑它们在不同应用场景下的表现。冒泡排序以简单易懂的实现而著称,适合初学者学习和理解排序的基本概念。不过,由于其较高的时间复杂度,当数据量较大时,性能显然不足。而选择排序则在交换次数上有所优势,更加适合大型数据的处理,但同样由于时间复杂度较高,不适用于实时系统或者对性能要求极高的场合。
选择排序在稳定性上也逊色于冒泡排序,虽然选择排序的实现可以进行改进,但一般情况下它不能实现稳定排序。因此,若存在对元素间相对顺序的要求,选择排序并非最佳选择。
五、排序算法的演变与发展趋势
随着计算机技术的不断进步,排序算法也经历了不断的演变。我们不难发现,冒泡排序和选择排序文件上相对简单易用,但在实际应用中已经不再是主流。快速排序、归并排序、堆排序以及基数排序等算法逐渐成为开发者的优选方案。这些算法的设计除了改进时间复杂度外,还更加关注内存的使用效率和稳定性,适应性越来越广泛。
在处理大型数据库时,快速排序因其O(n log n)的时间复杂度成为使用的首选。而对于实时动态数据,根据不同属性的分布并选择合适的排序算法,也让机器学习等领域的应用变得十分灵活。
在不断学习和探索的过程中,了解基本的排序算法仍然是编程的基础,只有真正掌握了这些基础概念,才能更好地理解更复杂的算法和数据结构并进行深入的运用。
欢迎大家在下方留言讨论,分享您的看法!
