干货满满的Dijkstra算法详解,你能否在最短时间内找到最优路径?
干货满满的Dijkstra算法详解,你能否在最短时间内找到最优路径?
亲爱的读者朋友们,今天我们将深入探讨一个对计算机科学至关重要的算法——Dijkstra算法。这不仅是一种解决最短路径问题的高效方法,还广泛应用于网络路由、地图导航等领域。这篇文章将带你逐步解析Dijkstra算法的每一个细节,帮助你掌握这一利器。
一、Dijkstra 算法简介
算法的重要性不言而喻,尤其是在现实生活中,比如你用的导航软件,背后就是算法在发挥作用。Dijkstra算法是由荷兰计算机科学家艾兹赫尔·迪杰斯特拉于1956年提出的,它的主要目标是解决单源最短路径问题。也就是说,给你一个起始点,如何找到到其他各个点的最短路径。
这个算法的关键点在于,它只适用于没有负权边的图,负权边的存在会导致结果的不确定性。想象一下,如果一条路的收费是负的,那你岂不是可以不断重复走这条路以节省费用吗?
二、Dijkstra 算法的核心理念
贪心策略是算法的核心,它意味着每一步都是基于当前信息做出最优决策,而且这个决策在未来可以引导我们找到全局最优解。结合了广度优先搜索(BFS)的特性,即便在复杂的图中,Dijkstra算法依然能迅速定位到最佳路径,这也是为什么它在各种应用中还是首选算法。
通过将图中的每个节点视为一个状态,我们可以利用“扩散”的方式逐步找到从起点到其他点的最短路径。这里的<|w|>扩散可以理解为对每一个节点进行更新,逐步扩展到未访问的节点。实际上,它通过一系列的操作,不断优化每个节点的“距离”,最终实现全图的最短路径计算。
三、算法步骤详解
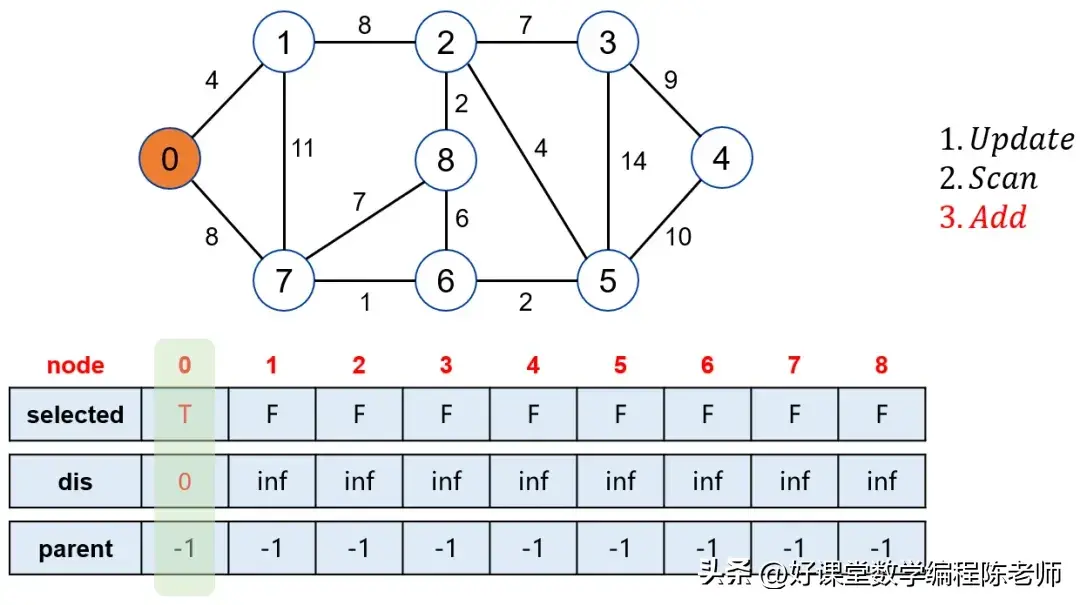
1. 初始状态设置
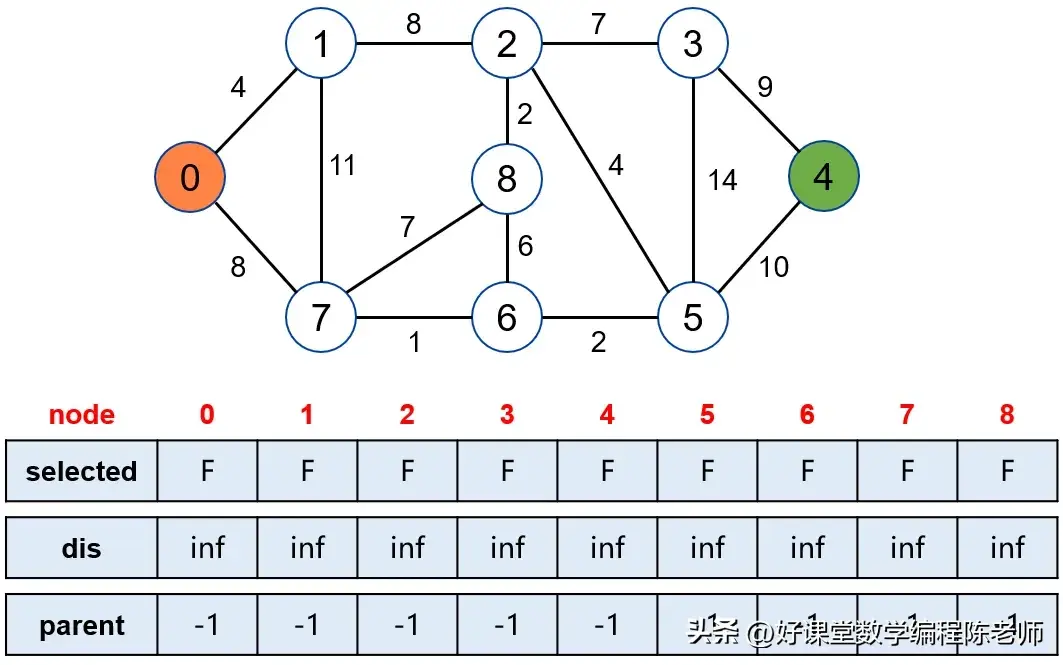
- 我们定义两个**:S(已确定最短路径的点)和U(未确定的点)。在开始时,S仅包含源点,而U则包含整个图中的所有其他点。
- 每个顶点的距离初始化:若顶点与源点相邻,距离为相应边的权值;否则,该顶点的距离设为 无限大(INF)。
- 这种初始化方式确保我们在算法运行时,能清晰地确定每个点目前的距离状态。
2. 选择最近的顶点
- 通过遍历《U》**,选出距离源点最近的顶点u,将其加入S**,意味着我们决定了从源点到u的最短路径。
- 一旦点u被选择并加入S,就会将其从U中移除,并进行距离更新。
3. 松弛操作
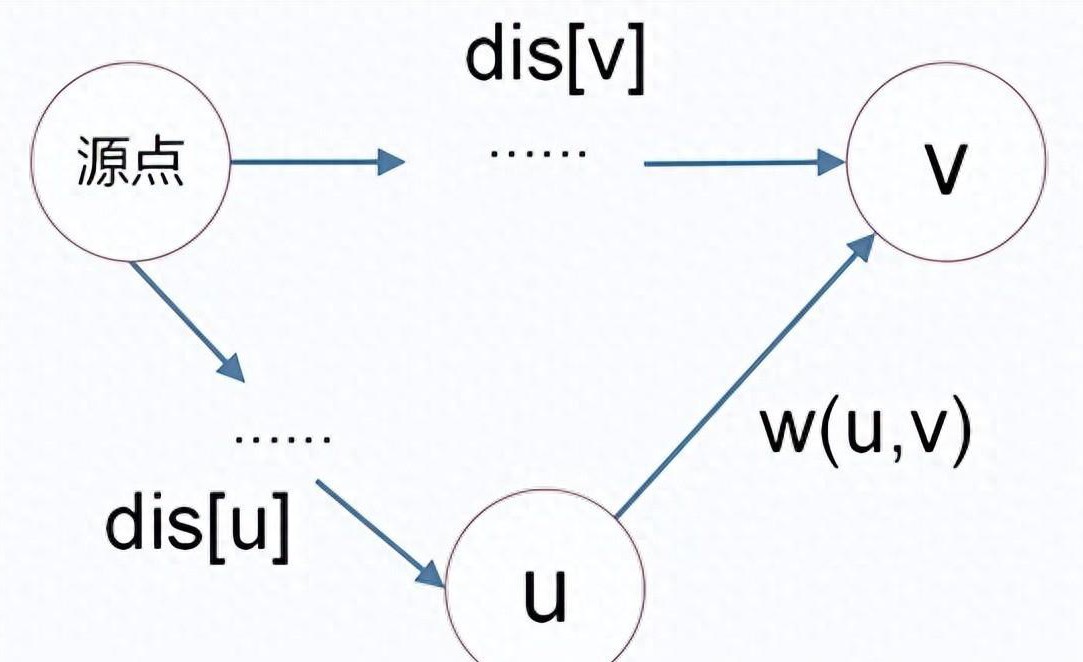
- 松弛操作是实现路径更新的关键,通过检查每个未访问点与已访问点的边权来进行距离更新。
- 公式:`if (dis[v] > dis[u] + w(u, v))`
- 如果点
- 注意:在执行松弛操作时,确保每个邻接点的更新都是基于最新的已知最短路径,这样才能确保结果的正确性。
四、Dijkstra 算法图解
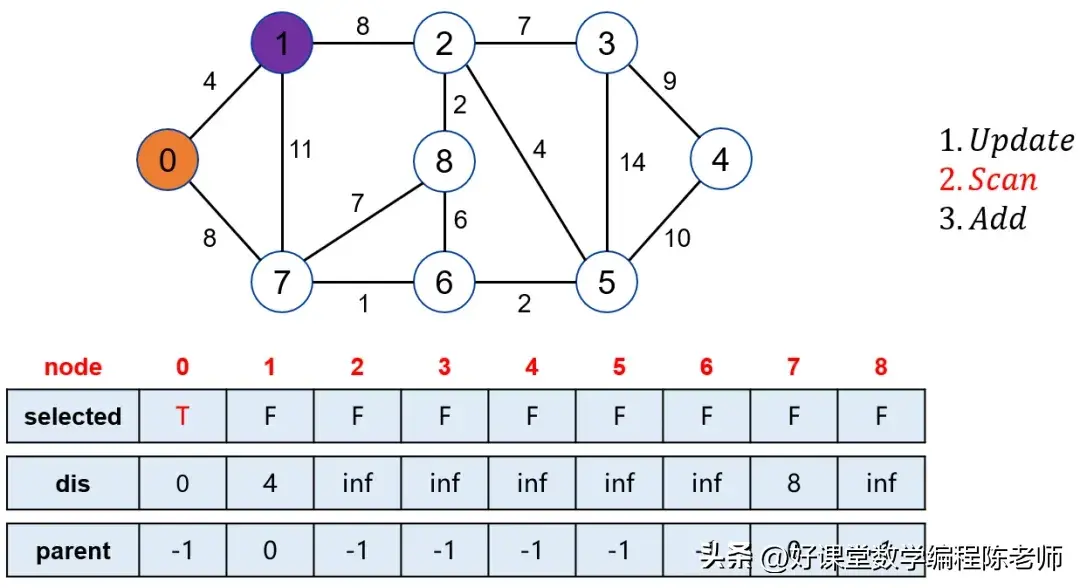
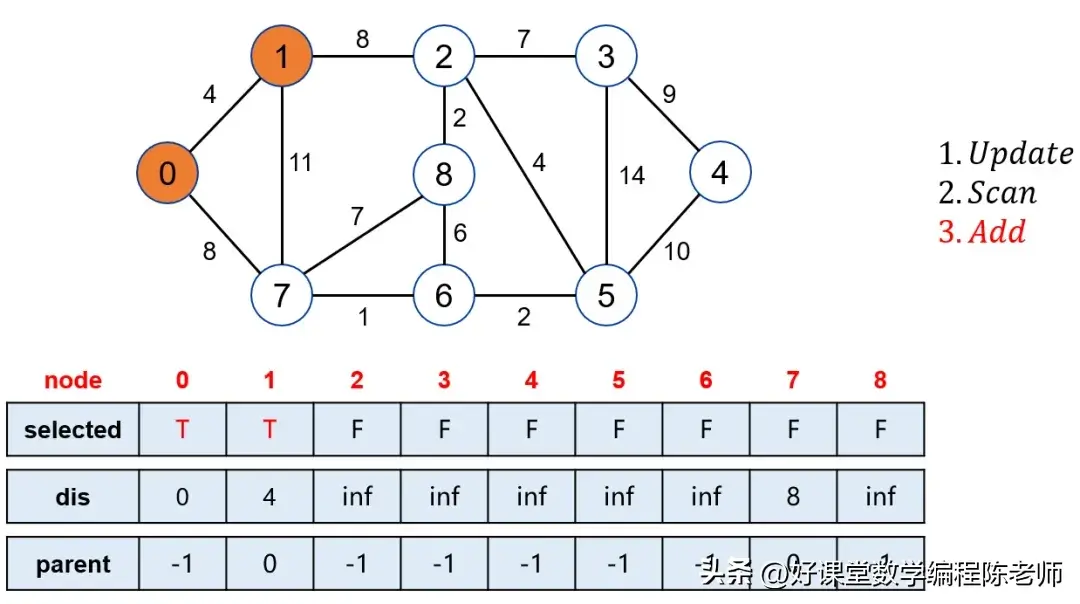
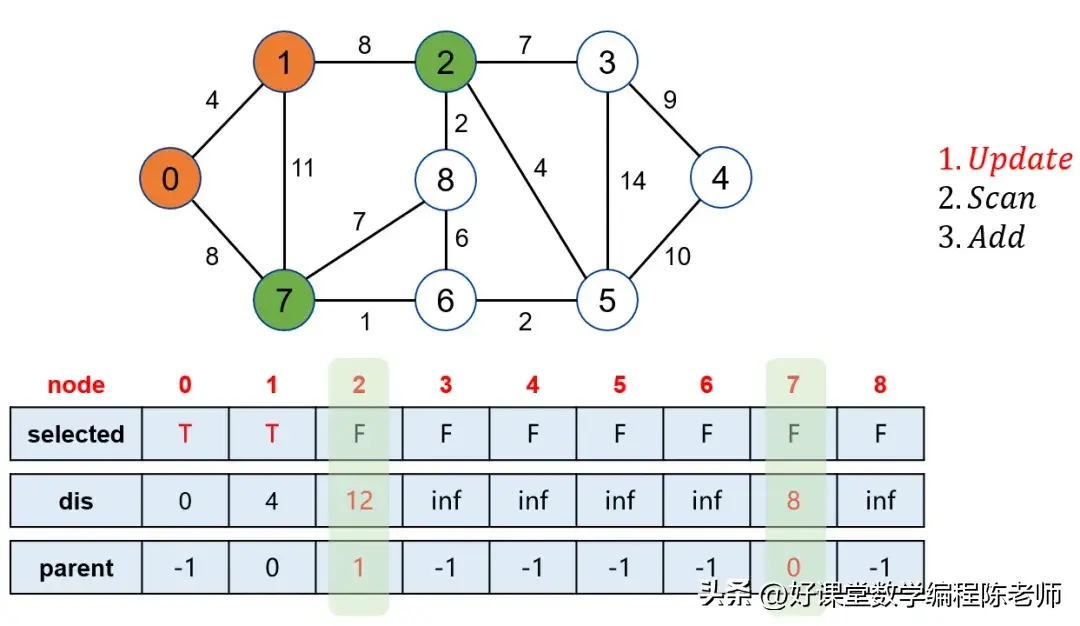
起点与终点的设定是算法图解过程中的重要部分。假设我们的起点是0,而目标终点是4。在初始化阶段,起点的距离为0,所有其他节点的初始距离为无限大。
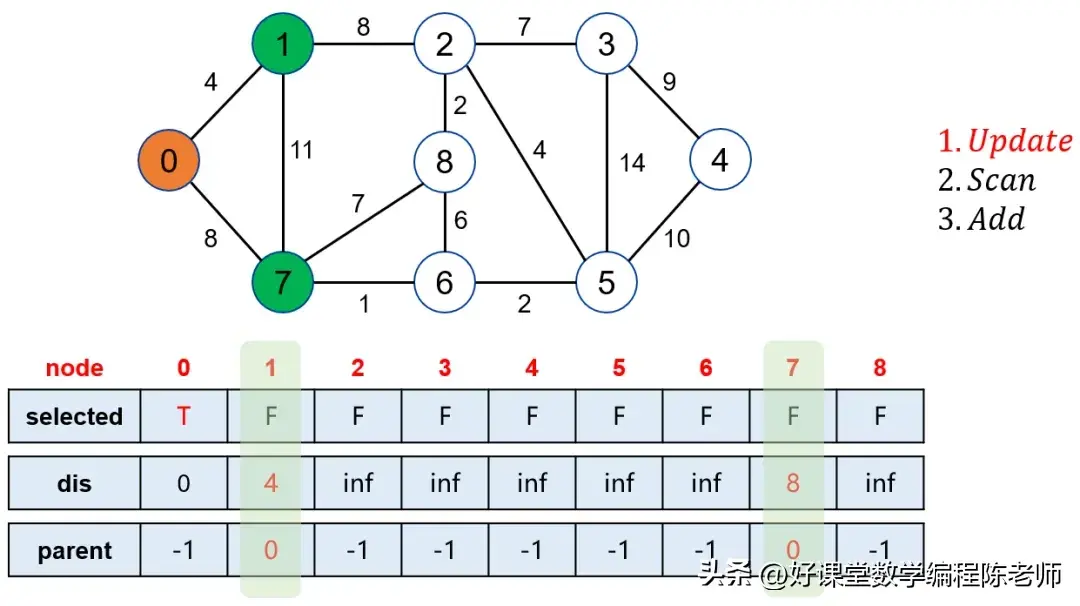
当我们选中点0后,松弛其邻接的点,比如1和7。此时,点0的邻接点距离会被更新。当我们寻找未被标记的点中距离源点最近的点时,经过几轮运算后,逐步标记1、7、6等。
作图的时候,可以与实际应用结合,如Google Maps的路线选择,这不仅是理论上的图,实际上是生活中处理路线问题的有效方式。
五、时间复杂度分析
分析Dijkstra算法时,首先要明确不同的实现方式会导致时间复杂度的变化:
1. 邻接矩阵的实现
- 时间复杂度为O(V^2),其中V是顶点的数目。对于小规模的密集图,使用邻接矩阵是非常直观且容易实现的。
2. 邻接表的实现
- 时间复杂度为O(E log V),其中E是边的数量。邻接表更适合处理稀疏图,且在大多数实际应用中广泛使用。
选择合适的数据结构不仅影响算法效率,更能在面对实际问题时大幅度提高程序的执行速度。
六、随堂检测
在学习完Dijkstra算法后,可以通过随堂检测来了解自己的掌握程度。例如,一个简单的选择题几乎能涵盖你对算法理解的整体情况。
在检测题目中,如果我问你,Dijkstra算法在查找最短路径时,他不能应用于边权值为负的图。这个问题可以考察到你对算法局限性的理解。
七、Dijkstra 算法的局限性
为什么边的权值不能为负数?这是因为,如果在路径计算过程中遇到负权边,它会导致之前已经确定的最短路径可能会被推翻。这就好像你走到了一个大城市的中心,然后发现你可以通过刚发现的小巷子绕过去,省下不少时间和金钱。
如果当前最短路径长度是8,而一个邻接点的边权是-15,再加上原本站在另一个点的距离20,这样一来,负权边影响了原有的解,导致你必须重新计算,这显然是不符合Dijkstra算法设计的逻辑。
八、编程实战
在实际编码中,Dijkstra算法的实现通常有两种方式:
1. 朴素版
- 使用邻接矩阵存储图,可以方便实现。其时间复杂度较高,但对学习入门非常有帮助。
```python
def dijkstra(graph, start):
V = len(graph)
dis = [float('inf')] V
dis[start] = 0
visited = [False] V
for _ in range(V):
u = min_dist(dis, visited, V)
visited[u] = True
for v in range(V):
if graph[u][v] and not visited[v]:
new_dist = dis[u] + graph[u][v]
if new_dist < dis[v]:
dis[v] = new_dist
return dis
```
2. 进阶版
- 使用邻接表和优先队列(如heapq),可以有效优化性能。
```python

import heapq

def dijkstra(graph, start):
V = len(graph)
dis = [float('inf')] V
dis[start] = 0
priority_queue = [(0, start)]
while priority_queue:
cur_dist, u = heapq.heappop(priority_queue)
for v, weight in graph[u]:
if cur_dist + weight < dis[v]:
dis[v] = cur_dist + weight
heapq.heappush(priority_queue, (dis[v], v))
return dis
```
这两种实现各有优缺点,但使用邻接表和优先队列的方式是现代编程中的优选方案,能大大提高算法的运行效率。
欢迎大家在下方留言讨论,分享您的看法!
