C++深度解析：K-means算法实现全攻略

详解C++实现K-means算法

一、引言

在数据处理和机器学习的领域里，K-means算法可谓是家喻户晓的明星。这种简单却高效的聚类算法，能够帮助我们快速地将数据划分为若干个集群，从而揭示数据的内在结构和规律。对于初学者来说，掌握K-means算法不仅是对聚类分析的入门，更是对机器学习算法原理的一次深入探索。

K-means算法的应用场景非常广泛，从商业智能到生物信息学，从图像处理到社交网络分析，都可以看到它的身影。它的基本原理是，通过迭代的方式，将数据点划分为K个集群，使得每个数据点与其所属集群的中心点（也称为质心）的平方距离之和最小。这种优化目标使得K-means算法在寻找数据集群方面具有出色的性能。

二、K-means算法原理

K-means算法的核心思想是通过迭代优化来找到最佳的集群划分。算法接受两个主要的输入参数：一是待处理的数据集，二是用户希望划分的集群数量K。算法的输出则是K个集群，每个集群都有一个中心点（质心），以及属于该集群的所有数据点。

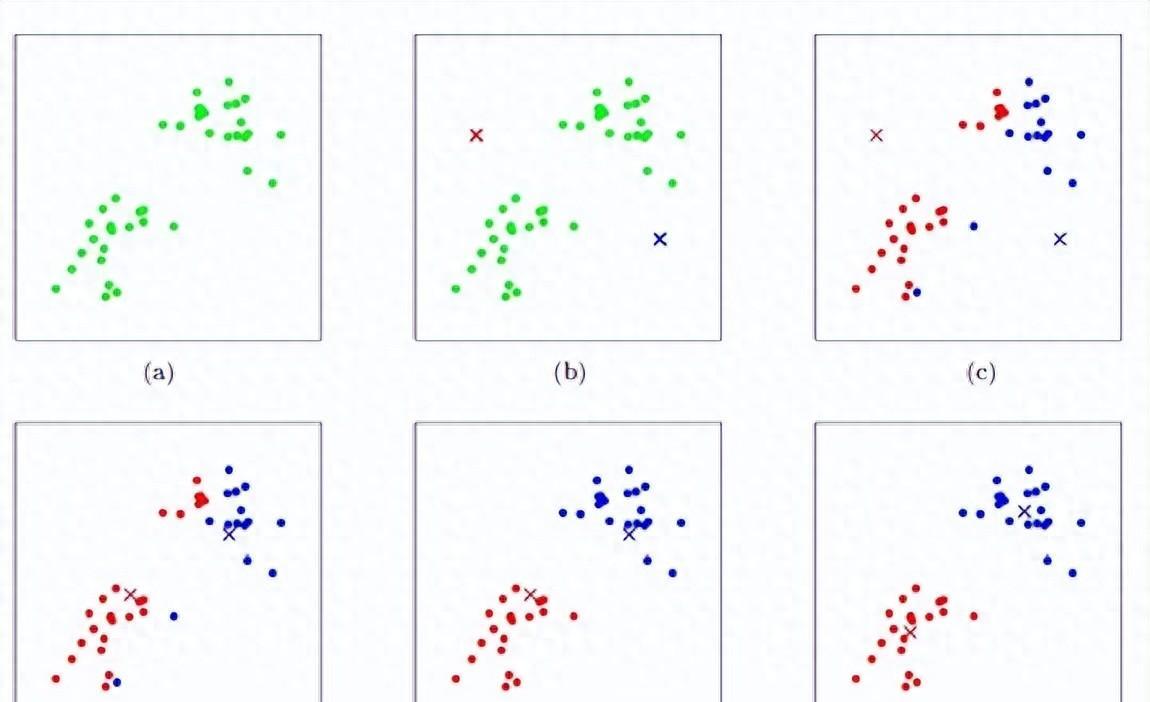
算法的执行过程可以概括为以下几个步骤：

初始化：随机选择数据集中的K个点作为初始质心。

分配点：对于数据集中的每个点，计算它与每个质心的距离，并将其分配给距离最近的质心所对应的集群。

重新计算质心：对于每个集群，计算其内所有数据点的平均值，得到新的质心。

检查收敛性：比较新旧质心的变化，如果变化很小（小于某个预设的阈值），则算法收敛，可以停止迭代；否则，更新质心并返回步骤2继续迭代。

通过这个过程，K-means算法能够逐步优化集群的划分，使得每个集群内部的点尽可能紧密，而不同集群之间的点则尽可能分离。

三、代码实现

接下来，我们将用C++来实现这个经典的K-means算法。我们需要定义一个Point结构体来表示二维空间中的点：

然后，我们需要实现计算两点间距离的函数。这里我们使用欧几里得距离作为度量标准：

接下来，我们需要实现计算点集质心的函数。质心是所有点的坐标平均值，可以通过遍历点集并累加坐标值来得到：

现在，我们可以开始实现K-means算法的主体部分了。这个部分可以进一步拆分为初始化、分配点、重新计算质心和检查收敛性几个步骤：

在主函数中，我们可以准备一个简单的数据集，并调用kmeans函数进行聚类：

四、案例与数据

假设我们有一个包含100个二维数据点的数据集，这些数据点大致分布在三个不同的集群中。我们设置K=3，并调用kmeans函数进行聚类。经过一定次数的迭代后，算**收敛到三个稳定的集群，并输出每个集群的质心以及属于该集群的所有数据点。

通过对比聚类前后的数据分布，我们可以清晰地看到K-means算法如何将原本混杂在一起的数据点划分成三个紧凑的集群。这种划分不仅有助于我们理解数据的内在结构，还可以为后续的数据分析和挖掘提供有力的支持。

五、总结与优缺点分析

K-means算法是一种简单而有效的聚类分析方法，它通过迭代优化的方式找到最佳的集群划分。在实际应用中，K-means算法已经被广泛应用于各种领域，取得了显著的效果。

K-means算法也存在一些缺点。它需要预先设定集群的数量K，这个值的选择往往需要根据实际问题和经验来判断。如果K选择不当，可能会导致聚类结果不佳。K-means算法对初始质心的选择比较敏感，不同的初始质心可能会导致不同的聚类结果。此外，K-means算法只能找到球形的集群，对于形状复杂的集群可能效果不佳。

针对这些问题，研究者们提出了一些改进方法。例如，可以通过多次运行K-means算法并选择最优结果来减轻对初始质心的敏感性；也可以使用其他更复杂的距离度量或聚类准则来改进算法的性能。

K-means算法是一种强大而灵活的聚类分析方法，它在处理大规模数据集时具有高效性和可扩展性。虽然存在一些缺点，但通过合理的参数选择和适当的改进方法，我们可以克服这些问题并得到满意的聚类结果。

在未来的研究中，我们可以进一步探索K-means算法的优化和扩展。例如，可以考虑将K-means算法与其他机器学习算法相结合，以实现更复杂的聚类任务；也可以针对特定领域的问题设计更合适的距离度量或聚类准则。此外，随着大数据和云计算技术的不断发展，我们也可以研究如何在大规模分布式环境下高效地实现K-means算法，以应对日益增长的数据处理需求。

通过不断的研究和实践，我们可以充分发挥K-means算法的优势，为数据挖掘和机器学习领域的发展做出更大的贡献。