如何用C语言实现一维线性插值,让你的数据分析逐步变得简单又精确?
如何用C语言实现一维线性插值,让你的数据分析逐步变得简单又精确?
亲爱的读者朋友们,数据分析在当今的科技界显得尤为重要。有很多小伙伴在进行数据处理时,也许会遇到插值的问题。今天,我将带你进入一维线性插值的世界,具体学习如何用C语言来实现插值,并与MATLAB的interp1函数进行对比分析,帮助大家全面理解这一技术运用的妙处和实践。我坚信,获取这些知识对你日后的工作和项目都会有极大的帮助!
一、引言
在现代数据处理与产品开发中,数据的准确性常常决定了项目成败的关键。而插值技术可以有效填补已知数据点之间的空缺,让分析的结果更加精准。一维线性插值是最常用的插值方法,因为它的数学原理简单易懂,同时编程实现也相对容易。在本文中,我们将深入对比C语言的插值实现和MATLAB的interp1函数,通过丰富的实例和详实的数据,让你更好地掌握这一技术。
二、一次函数的5种形式
一次函数是一种基本的线性关系,它可以有多种表达形式,主要包括斜截式、点斜式、一般式等。理解这些形式对于我们后续的插值计算至关重要。
1. 斜截式 y = mx + b
- 在该式中,m代表斜率,b为截距。这种形式在执行插值时,容易明白不同点间的变化速度,适用于简单的线性关系。
2. 点斜式 y - y₁ = m(x - x₁)
- 这个公式更加灵活,适合在已知某一点的情况下进行插值。比如,当你只知道某个数据点及其斜率时,可以用这个形式进行估算。
3. 一般式 Ax + By + C = 0
- 这种形式适合于多维的直线方程,但在一维插值时同样可以为我们提供视角,特别在多点数据集的情况下,可以进行多线性回归分析。
理解了这些基础知识,我们才能在实际的编程应用中更加游刃有余。在后续中,可以根据具体情况选择合适的函数形式进行数据插值。
三、C语言的一维线性插值程序
使用C语言进行一维线性插值的实现相对简单。我们需要用到一组已知的数值来推算未知的数据点。假设我们有如下的数据:
- 已知数据点:
x: 2, 5, 8, 20
y: 200, 300, 400, 700
目标是求当x = 4时对应的y值。在实现的过程中,有几个关键步骤需要注意。
1. 数据准备
- 在代码中我们需要定义一个数组来存储x和y值,并确保这些数据是有序排列的。这让插值计算更有效率。
2. 插值算法
- C语言通过简单的算法来找到对应的y值:
$$ y = y_1 + (y_2 - y_1) \times \frac{x - x_1}{x_2 - x_1} $$
这个公式由较小x值和较大x值之间的值推导出y。需要注意的是,确保所选择的两个已知点与待插值点相邻,以防止插值结果的不准确。
3. 程序示范
```c
include
float linearInterpolation(float x, float x0, float y0, float x1, float y1) {
return y0 + (y1 - y0) (x - x0) / (x1 - x0);
}
int main() {
float x[] = {2, 5, 8, 20};
float y[] = {200, 300, 400, 700};
float x_to_interpolate = 4;
float result;
// 查找相邻的x值
for (int i = 0; i < 3; i++) {
if (x[i] <= x_to_interpolate && x[i+1] >= x_to_interpolate) {
result = linearInterpolation(x_to_interpolate, x[i], y[i], x[i+1], y[i+1]);
break;
}
}
printf("The interpolated value at x = %.2f is y = %.2f\n", x_to_interpolate, result);
return 0;
}
```
4. 运行结果
- 编译运行后,输出结果为y = 250,说明在x = 4时,对应的y值为250。这个过程展示了C语言插值的基本原理与实现。
四、MATLAB的interp1函数
MATLAB是数据处理与分析中不可或缺的工具,而其内置的interp1函数提供了便捷的一维插值方法。了解如何使用这个函数能够显著提高你在数据分析中的效率。
1. 插值函数介绍
- interp1是MATLAB中的一维插值函数,提供多种插值方式,如线性、最近邻、立方等。
- 语法格式为:
```matlab
yi = interp1(x, y, xi, method)
```
其中,x与y为已知数据,xi为插值点,method为选用的插值类型(如'linear'、'nearest'等)。
2. 与C语言实现的对比
- MATLAB的interp1函数在使用上更加直观友好,用户只需传入数据和插值点即可,而C语言需要自行处理数组和循环。
- 另外,interp1函数内部进行了一些数值优化,可以处理更复杂的插值需求,对于大型数据的插值计算,MATLAB能够提供更快的计算速度。
3. 实例实践
```matlab
x = [2 5 8 20];
y = [200 300 400 700];
xi = 4;
yi = interp1(x, y, xi, 'linear');
disp(['The interpolated value at x = ' num2str(xi) ' is y = ' num2str(yi)]);
```
结果将显示y = 250,验证与C语言插值结果一致,简化了计算过程。
五、不同插值方法的特点
插值方法有多种,选择适合的算法可以大幅提升效果。在不同场合下,选择不同的插值方法能保持数据的精准性和计算的效率。
1. 3次埃尔米特插值
- 这种插值方法不仅考虑函数值,还考虑导数的值。因此,它能够保证插值结果的光滑性,特别适用于需要保持更高精度的场景中。
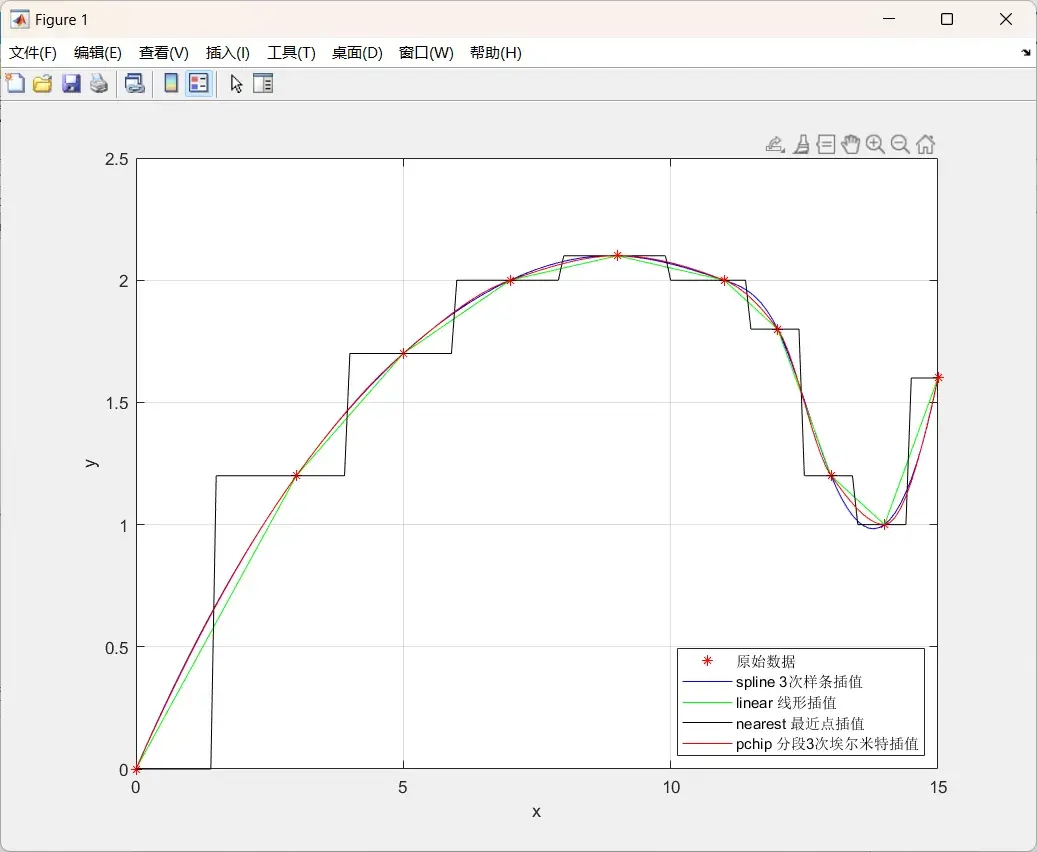
2. 3次样条插值
- 相比于其他方法,三次样条插值对解的连续性要求更高,它保证了函数的二阶导数在节点处也连续。通过这种方式,我们能获得更为平滑的插值曲线,实现了更高级别的拟合。
3. 实例分析
- 实例1:
使用MATLAB的样条插值方法进行较为复杂的曲线拟合,此时x与y的数量级和趋势更为复杂,确保样条插值的优势。
- 实例2:
场景模拟,如天气变化的趋势分析,你可以使用C语言的三次样条插值进行耗时与性能的详细对比,观察性能差距及影响。
六、参考内容
在准备这篇文章时,参考了多篇网络文献,其中包括《用C语言实现MATLAB的一维插值函数interp1》。如果你想深入了解或获取更具体的代码示例,推荐访问相关专业论坛和资源网站,例如:GitHub上相关的开源项目以及在线编程教程。
---
希望今天的分享能让你对于一维插值的理解更加深入,特别是在数据处理与分析中的应用。欢迎大家在下方留言讨论,分享您的看法!
