解密KL散度:千万人都在谈论的概率分布变化背后的秘密
解密KL散度:千万人都在谈论的概率分布变化背后的秘密

亲爱的读者朋友们,您是否曾对数据分析中的“KL散度”感到困惑?在信息论和机器学习的海洋中,KL散度如同一盏明灯,照亮了概率分布的奥秘。今天,我们将一起深入探讨KL散度以及相关散度概念,带您领略这一领域的魅力。
一、引言
在现代科技迅猛发展的背景下,信息论、机器学习、统计学成了许多计算问题的基础。KL散度(Kullback-Leibler Divergence)作为其中一个重要的概念,能够为我们量化概率分布之间的差异,为数据科学及机器学习的深入研究和实际应用提供强有力的支持。它不仅是理解数据如何呈现与变化的核心工具,也是许多算法优化和应用的关键。在接下来的篇幅中,我们将层层剖析KL散度的定义、计算方式、自身特性及其在各行各业的实际应用。
二、KL散度的定义与计算
KL散度的基本概念令人耳目一新。它被定义为两个概率分布之间的相对熵,主要用来衡量真实分布P与近似分布Q之间的信息损失。在实际操作中,我们可以用数学公式来进行计算。KL散度从数学上定义为:
1. 对于离散分布,其计算公式为:
\[
D_{KL}(P || Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}
\]
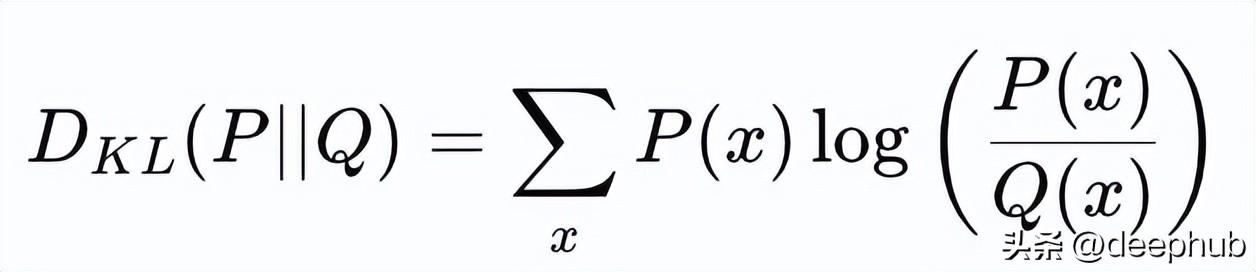
2. 对于连续分布,其计算公式为:
\[
D_{KL}(P || Q) = \int p(x) \log \frac{p(x)}{q(x)} dx
\]
P(x)和Q(x)分别代表真实分布和近似分布。这样的定义让计算变得简单易懂。尤其是对于大数据环境中经常出现的复杂概率分布,KL散度帮助我们清晰地量化模型所引入的误差。
KL散度的理解也是至关重要的。当我们使用一个概率分布Q去编码另一个分布P的数据信息时,KL散度衡量了由此引起的信息损失。这一点在数据压缩领域尤为明显。例如,在图像压缩中,我们希望使用更少的比特数来存储尽量多的信息,KL散度便可以用来评估不同压缩算法的效率,使得编码方案的选择变得更加科学合理。
三、与熵的关系
熵的概念是信息论中的重要组成部分,香农熵被定义为衡量具有不确定性或随机性的量。其公式为:
\[
H(P) = -\sum_{x} P(x) \log P(x)
\]

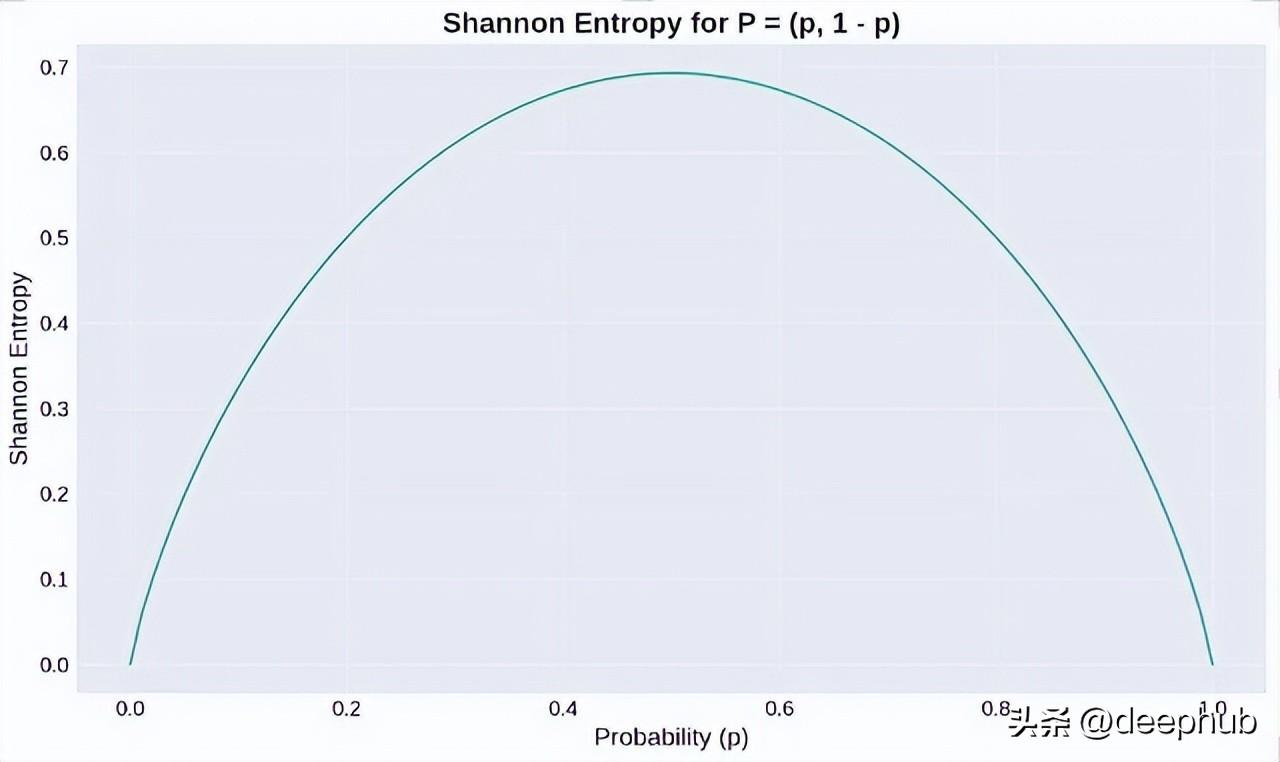
熵可以看作是信息的度量,熵越大表示信息的不确定性越高。例如,在二元分布中,当概率p=0.5时,熵达到最大,意味着最大的随机性和不确定性。
从熵推导出与KL散度的关系,能够进一步深化对两者的理解。具体来说,KL散度可以看作是P的熵减去P与Q之间的“交叉熵”。这意味着KL散度实际上是在衡量用Q分布编码P的额外不确定性。这样的理解不仅有助于理论研究,也在模型优化和参数调优中扮演着关键角色。
四、KL散度的特性
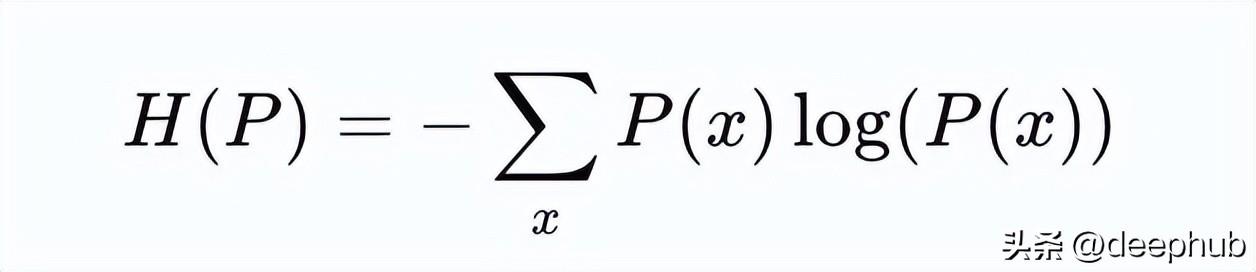
非负性是KL散度的一项重要特性。它的值永远不会小于零,只有在分布P和Q完全相同的情况下,KL散度才会等于零。这一特性在很多实际场景中都有着极为重要的应用,比如在机器学习的损失函数中,通过监测KL散度来调整模型参数,使得模型更加精准。此外,KL散度的非负性也使得我们在进行概率模型训练时更为稳妥,不必担心引入负值带来的复杂性。
另一特点是不对称性,即D_{KL}(P||Q)与D_{KL}(Q||P)的值通常是不相等的。这一特点与其他距离度量的对称性质形成了鲜明对比。正因如此,KL散度在某些场合下更能反映出真实数据模型的偏好。例如,在自然语言处理任务中,KL散度被用来衡量生成模型与真实文本分布之间的差异,为生成对抗网络(GAN)提供了有效的反馈机制。
五、KL散度的应用实例
KL散度的实际应用是相当广泛的,尤其是在变分自编码器(VAE)中,KL散度充当了正则化器的角色,确保潜在变量分布(通常是标准高斯分布)与我们设定的先验分布尽量接近。通过这种方式,VAE能够生成新的数据样本,且新生成的数据能够充分保留真实数据的特征。
在数据压缩领域,KL散度也有着极为重要的角色。当应用于图像或文本数据时,KL散度能够量化不同压缩算法的表现,使数据存储和传输更加高效。在强化学习中,KL散度被广泛应用于策略优化过程中,例如在近端策略优化(PPO)算法中,它帮助控制新旧策略之间的偏差程度,以实现更稳定的训练效果。
数据漂移检测也是KL散度的一个重要应用场景。在工业界,例如一些电子商务平台,用户行为的概率分布很可能随着时间的推移而变化。这种分布迁移会显著影响推荐系统和广告投放策略。通过对数据流的实时监测,企业可以及时采集到关于KL散度的信息,快速应对市场变化,调整策略,有效提升了业务的整体水平。
六、其他相关散度概念
除了KL散度外,还有几个重要的散度概念值得关注,其中Jensen-Shannon散度(JS散度)是一种对称的散度度量。它的定义通过KL散度建立,但克服了KL散度不对称的局限性,给定两个概率分布P和Q,JS散度计算如下:
\[
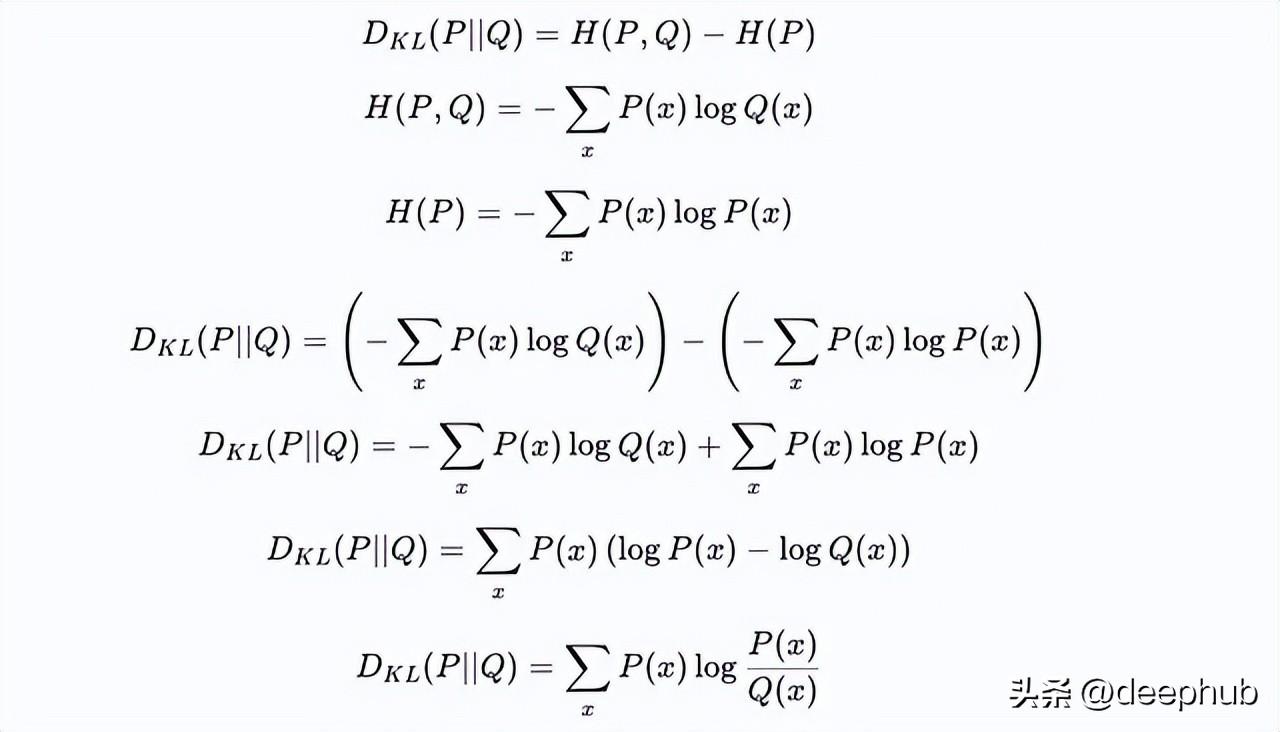
D_{JS}(P || Q) = \frac{1}{2} D_{KL}(P || M) + \frac{1}{2} D_{KL}(Q || M)
\]
M是P与Q的平均分布。JS散度为不对称的KL散度引入了平衡的视角,为需要无偏比较的场景提供了有效解决方案。例如,在文本相似性检索中,JS散度被广泛用于比较不同文档的主题相似性,从而提升检索的准确率。
Renyi熵则是香农熵的拓展形式,它为我们提供了一种灵活的方式来衡量不确定性。Renyi熵通过参数α控制,并依据不同的α值反映不同的信息聚焦。例如,当α < 1时,它更关注稀有事件,而当α > 1时,则更加重视常见事件。这样的灵活性使得Renyi散度在差分隐私和数据保护中的应用愈发重要,帮助我们在保护用户隐私业务中,合理控制数据共享的风险。
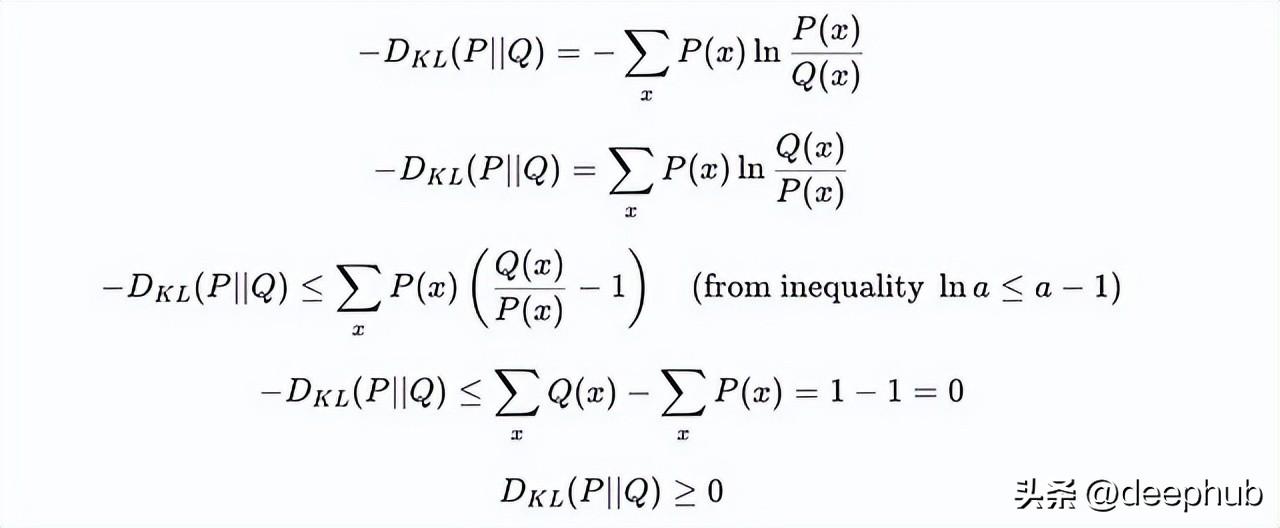
七、实际案例分析
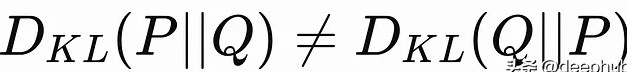
在电子商务领域,用户行为的概率分布随时间发生变化的情况并不少见。以一个电子商务平台为例,该平台持续跟踪客户在五个产品类别中的购买行为:电子产品、服装、图书、家居与厨房、玩具。每周收集的点击比例数据可以用概率分布的方式呈现,从而便于我们更好地分析用户行为的演变。
我们可以运用KL散度对数据进行详细分析。首先,记录每周的点击比例数据,计算KL散度,监测变化趋势。数据分析发现,从第1周到第2周,看到轻微漂移,特别是第二类别(服装)的点击比例略有上升;在第3周,服装类别的主导地位进一步增强,最终在第5周至第7周,影响达到显著程度,其点击份额一直上升,而电子产品类别则显著下降。
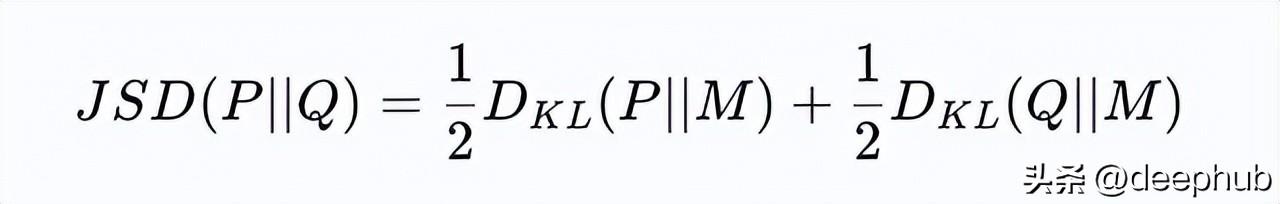
通过对KL散度、JS散度和Renyi散度的不同衡量,我们可以迅速捕捉到用户兴趣的变化。例如,当我们选择α = 0.5的Renyi散度时,它对低概率类别(如家居与厨房、玩具)敏感,能够提前捕捉到这些类别的浮动情况。而当设置α = 2时,更加突显了服装类别的持续增长,帮助企业在适当时机进行精准的市场策略调整。
这样的案例展示了如何将理论概念运用到实际场景中,通过综合运用这些工具,企业可以更精准地把握市场动态,以数据驱动的方式做出明智的决策。
八、展望未来
随着大数据时代的不断发展,KL散度与其他散度概念的价值愈发明显。在许多领域,包括金融风险评估、生物信息学、自然语言处理等,散度指标都展现出了巨大的应用潜力。未来,在量子计算、复杂网络分析等新兴领域,KL散度及其相关概念定会找到新的应用场景。
最新的研究持续提出这些概念的新变体与扩展,以应对日益复杂的数据分析挑战。在这样的背景下,掌握KL散度及其相关概念,不仅能帮助我们更深入地理解和分析复杂的数据世界,还能为之后的科学研究和技术创新提供强大支持。
欢迎大家在下方留言讨论,分享您的看法!
