KNN分类算法：机器学习中的明星之选！

机器学习入门：KNN分类算法详解

在机器学习的广阔领域中，K最近邻（KNN）算法以其简洁直观的原理和出色的性能，成为了初学者和资深工程师都乐于使用的一种分类算法。今天，就让我们一起揭开KNN的神秘面纱，探索其背后的技术奥秘。

一、KNN算法初识

KNN，全称为K-Nearest Neighbors，是一种基于实例的学习算法。简单来说，KNN算法就是通过测量不同数据特征值之间的距离来进行分类。它的工作原理是：存在一个样本数据**，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们只选择样本数据集中前K个最相似的数据，这就是K-近邻算法中K的出处，通常K是不大于20的整数。选择K个最相似数据中出现次数最多的分类，作为新数据的分类。

KNN算法最大的优点就是简单易懂，易于实现，无需估计参数，无需训练。但与此它也有一些缺点，比如当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数，从而导致预测错误。此外，KNN算法的计算量较大，特别是当特征维度较高时，计算距离会变得非常耗时。

二、KNN算法的工作原理

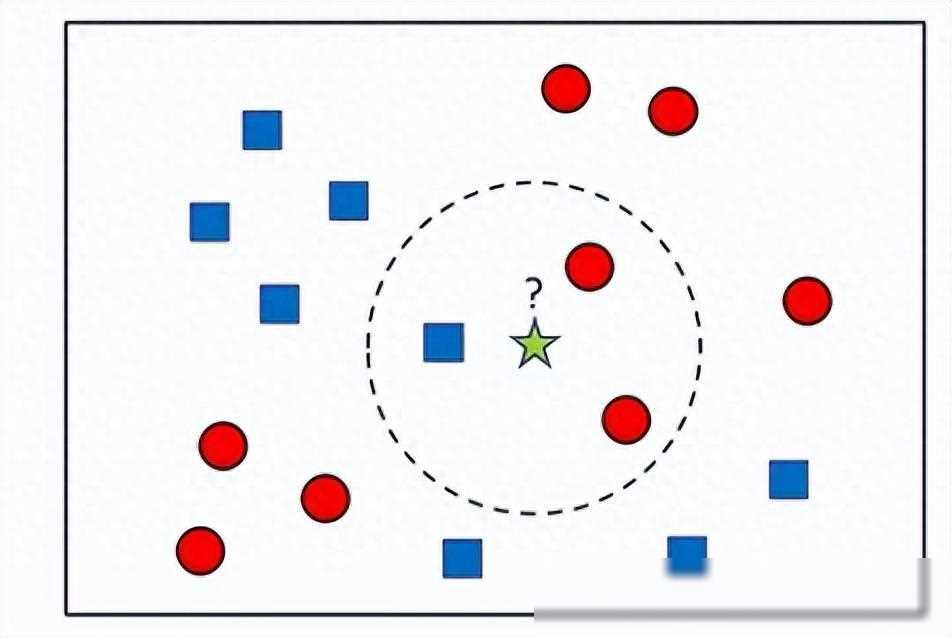
KNN算法的核心思想就是“近朱者赤，近墨者黑”。它假设在特征空间中，如果两个样本点的距离较近，那么这两个样本点就更可能是属于同一个类别。因此，对于一个新的样本点，我们可以计算它与训练集中所有样本点的距离，然后找出距离它最近的K个样本点，这K个样本点中出现次数最多的类别就是这个新样本点的预测类别。

在KNN算法中，距离的度量是一个非常重要的因素。常用的距离度量方式有欧氏距离、曼哈顿距离、切比雪夫距离等。其中，欧氏距离是最常用的一种，它表示在m维空间中两个点之间的真实距离。

三、KNN算法的应用场景

KNN算法在实际应用中有着广泛的用途。以图像识别为例，当我们需要识别一张图片中的物体时，可以将图片中的每个像素看作一个特征，然后将这些特征输入到KNN算法中进行分类。由于KNN算法不需要构建复杂的模型，因此可以快速地处理大量的图像数据。

此外，KNN算法还可以用于文本分类、推荐系统等领域。在文本分类中，我们可以将文本中的每个单词或短语看作一个特征，然后将这些特征输入到KNN算法中进行分类。在推荐系统中，我们可以将用户的历史行为数据（如浏览记录、购买记录等）作为特征，然后使用KNN算法找出与当前用户最相似的其他用户，并将这些用户喜欢的物品推荐给当前用户。

四、KNN算法的优化与扩展

虽然KNN算法简单易懂，但在实际应用中仍然需要进行一些优化和扩展。以下是一些常见的优化和扩展方法：

选择合适的K值：K值的选择对KNN算法的性能有着重要影响。如果K值过小，可能会导致过拟合；如果K值过大，可能会导致欠拟合。因此，我们需要根据具体的应用场景和数据集来选择合适的K值。

使用加权KNN：在标准的KNN算法中，所有邻居样本的权重都是相同的。但在实际应用中，我们可能会希望离目标样本更近的邻居样本具有更大的权重。因此，可以使用加权KNN算法来改进性能。

使用距离加权：除了对邻居样本进行加权外，还可以对距离进行加权。例如，可以使用反比于距离的平方的权重来计算邻居样本的权重。这样可以使得离目标样本更近的邻居样本具有更大的影响力。

特征选择：在特征维度较高时，计算距离会变得非常耗时。因此，可以通过特征选择来降低特征维度，提高算法的运行效率。常用的特征选择方法有主成分分析（PCA）、线性判别分析（LDA）等。

使用KD树或球树：为了提高KNN算法在大数据集上的运行效率，可以使用KD树或球树等数据结构来存储训练样本集。这些数据结构可以快速地找到距离目标样本最近的K个邻居样本。

五、结语

KNN算法作为机器学习领域中的一种基础算法，不仅简单易懂、易于实现，而且在实际应用中具有广泛的用途。通过对其原理、应用场景以及优化扩展方法的深入了解，我们可以更好地掌握这一算法，并将其应用于实际项目中。我们也要意识到KNN算法并不是万能的，它也有其局限性和适用场景。因此，在实际应用中需要根据具体