三体问题的突破:Transformer如何解决132年数学难题?
三体问题的突破:Transformer如何解决132年数学难题?
亲爱的读者朋友们,今天让我们一起深入探讨一个激动人心的话题——Transformer如何成功破解被困扰了132年的李雅普诺夫函数问题。你是否曾想过,宇宙中那复杂的三体运动背后,隐藏着哪些未解的数学秘密?而在这些秘密的最终揭开时,人工智能又扮演着怎样的角色?接下来,我们将逐一揭开这些谜团。
一、引言
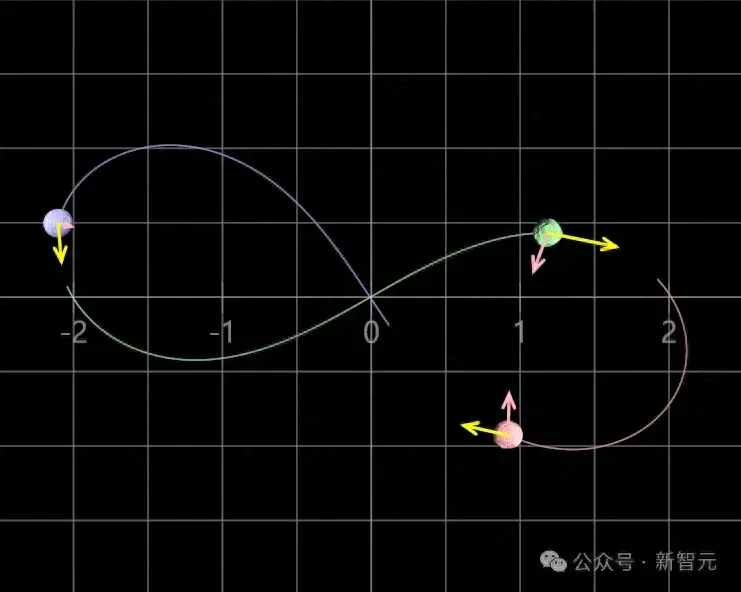
在现代科学史上,三体问题始终占据着举足轻重的地位。几乎每位物理学家或数学家都曾在这道题目面前"碰壁"。它并不仅仅是几个行星、星体相互之间引力影响的运动规律,而是一个涉及到复杂非线性动力学的挑战。为了更深入地理解这一点,我们必须提到李雅普诺夫函数,这是评估系统稳定性的一个关键工具。在无数次试探中,数学家们不断追寻能够通用的解法,却始终未能触及其核心。
近来,一个崭新的研究给我们带来了突破的希望。Meta AI的研究团队通过其独特的Transformer模型,意外地为这一困境提供了解决方案。他们的研究成果获得了NeurIPS 2024的接收,令人振奋。接下来的部分将带您了解三体问题及其数学挑战所蕴含的深意。
二、三体问题及其数学挑战

三体问题的概念来源于经典的天体力学研究。它的挑战在于,当三个物体处于万有引力作用的影响下,始终无法找到一个简单的解析解。实际上,所有的尝试都告诉我们,对于任意配置的初始条件,系统的未来运动轨迹往往是不确定的。这意味着,无论是哲学家还是科学家,都不得不接受其"混沌"的本质。
李雅普诺夫函数,正是为了解决这种不确定性而产生的。在1892年,俄国数学家李雅普诺夫首次提出这个概念,他证明,只要找到一个特定的函数V在平衡时具有严格的最小值,并且在无穷远处具有无限大,系统将会保持稳定。然而,理想与现实之间的鸿沟在于,未能通用的求解方法使这一理论只停留在纸面。
这使得李雅普诺夫函数的存在成为一个开放而复杂的数学难题。对于想要深入了解动力学的研究人员来说,这无疑是一个巨大的挑战。实际案例中,如天体物理学家们在研究行星运动时,便会发现每一次的计算都可能因初始条件的微小变化而导致全然不同的结果。这一现实长久以来让科学家们体会到了数学的无情。
三、Meta AI的研究成果
在这样一个庞大的数学迷雾中,Meta AI的研究无疑是闪亮的一束光。他们带来了名为Transformer的强大模型,专门针对寻找李雅普诺夫函数这一难题展开研究。通过大量的数据训练,研究者们探索各种动力系统的行为,通过不断的迭代,成功发现了多个稳定系统及其对应的李雅普诺夫函数。
研究的方法主要是通过采样和生成技术,以优雅的方式解决这个问题。研究团队利用后向生成技术生成动力系统,最终取得了令人瞩目的成果。这意味着,借助于现代AI技术,曾经困扰广大数学家的问题有了实际应用的可能性。
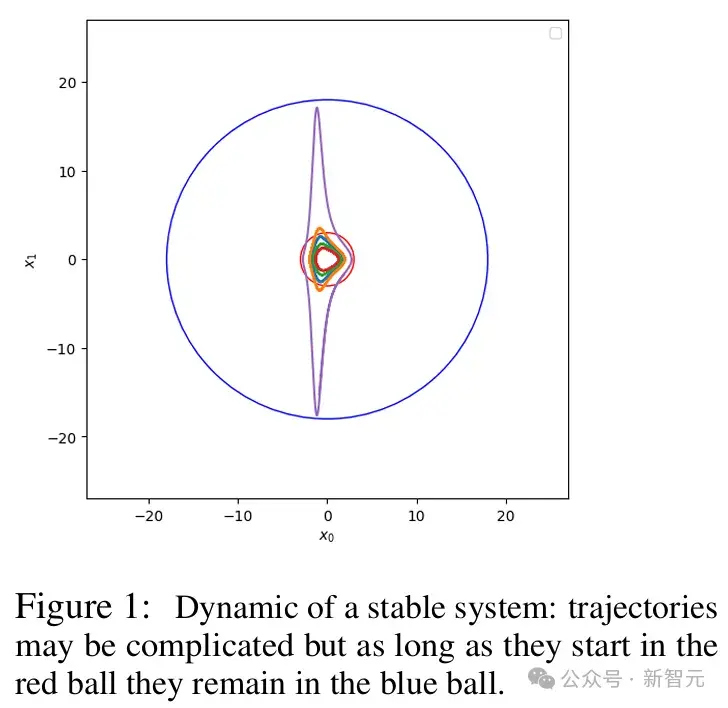
在论文的结尾,研究者强调并不认为Transformer在进行传统意义上的推理。相反,研究发现其可能通过一种"超级直觉"来解决问题。具体而言,这是一种基于模型对大量数学问题的深刻理解,通过恰当选择训练样本,使得模型在面对复杂问题时,能够得出正确的结论。
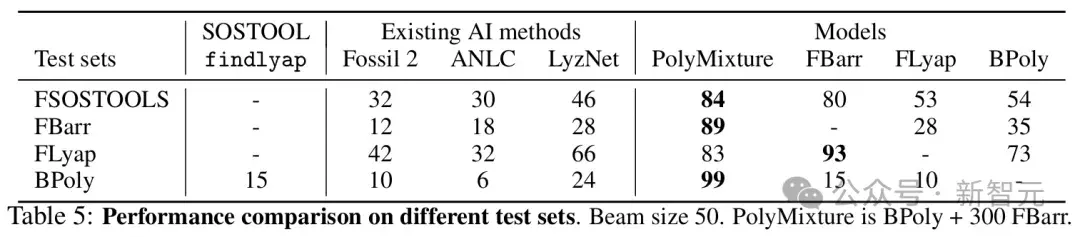
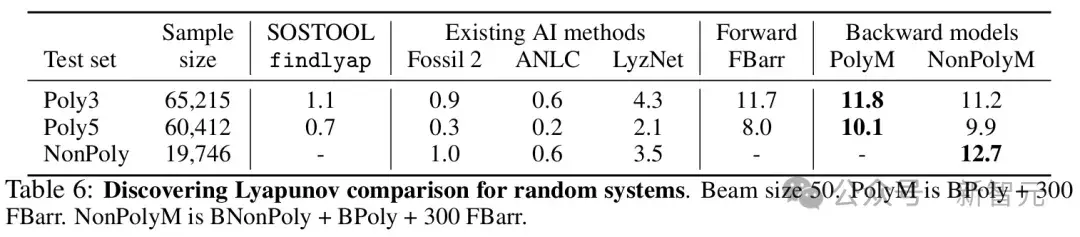
在他们的实验中,模型在随机生成的多项式系统中找到李雅普诺夫函数的准确率已超过了80%。这让人惊叹,因为在同样的任务中,硕士生级别的人类数学家的准确率不足10%。这一差距再次重申了现代AI在深刻理解复杂问题上的巨大潜力。

四、动力系统稳定性的基础理论
稳定性是动力学理论的基石,而李雅普诺夫函数则是理解其抗拒性的重要工具。随着时间的推移,许多数学家试图阐明系统的稳定性,以保证在扰动发生时,系统能够维持其结构。这一点在18世纪的牛顿和拉格朗日的论文中均有涉及,那时,经过众多有识之士的探索,稳定性问题逐渐得到了广泛重视。
李雅普诺夫函数为我们提供了一种判断系统稳定性的重要标准。根据李雅普诺夫的理论,如果一个函数V可以在平衡点附近显示单调递减的趋势,那么我们就可以预期系统的行为是稳定的。这一发现不仅适用于基本的物理系统,还为复杂生态系统、工程设计等多领域提供了理论基础。
而在实践中,数学家们通常也会尝试使用数值方法来寻找李雅普诺夫函数的近似解。例如,基于数值优化的算法,构建稳定性评估工具,帮助决策者在各种领域做出更为合理的方案。这些方法不仅适用于数学,还广泛应用于控制系统设计、气象气候模型等重要领域,提升了系统的灵活性与自适应能力。
利用AI这种新技术来寻找李雅普诺夫函数的价值正在显露。这种新方法极大地拓宽了潜在的研究领域,研究人员能够探索更多尚未解决的数学问题,并将其应用于实际情况中。
五、Transformer模型的训练与测试
这项研究显示,Transformer模型在处理复杂的数学问题时,展现出惊人的能力。那么,该模型是如何训练和测试的呢?
研究团队通过序列到序列的Transformer来在给定的输入(动力系统)和输出(李雅普诺夫函数)之间进行推导。在具体步骤上,研究者结构化地处理数据,确保信息充分利用。从生成的系统与李雅普诺夫函数对中获取样本,这样的配对不仅降低了数据处理的复杂度,还有助于提高模型的泛化能力。
在实验设置上,研究者使用了多种不同的超参数配置,包括8层深度的网络和640维的嵌入维度。他们还采用了Adam优化器,以保证模型的收敛性。在这一过程中,不同批次的样本数值变化控制得当,以避免模型过拟合。而在训练过程中,每个epoch处理240万样本,使模型逐步积累经验。通过如此精细的调校,最终实现了在分布外测试集上值域精度高达73%至75%。
当研究者在多项式系统中进行测试时,发现模型对随机生成的系统能够达到接近完美的准确率。这一成就标志着AI技术对复杂问题解析能力的巨大提升,同时为进一步应用该技术奠定基础。

分析过程中,研究者还发现了模型在面对反向生成数据时可能存在的偏差,表明在不同分布之间,模型的学习过程可能会受到影响。因此,他们引入了少量已知解决方案的正向示例,利用这个自我增强的方法,显著提升了模型准确率。
六、研究的启示与未来方向
通过这一系列的实验与研究,研究者明确指出了当今AI技术在解决基础科学难题中的潜力。对于许多科学家而言,是否真的能够创建出一个完美的模型来模拟复杂的物理现象,仍然是一个悬而未决的问题。虽然对此AI提供的解决方案仍有疑虑,但缓慢演进的过程正在向更为可观的方向发展。
从这一研究中得出的重要观点是,AI的推理能力并非传统意义上的“推理”,而是展现出一种超乎寻常的直觉能力——这使得模型能够在极为复杂的问题中找到“聪明的解”。其背后是对数据的深刻理解,而非机械地复述。
科研者们计划将这种模型扩展到更大的数据集和更复杂的系统中,探索如非多项式系统的问题。根据目前的进展,有理由相信,人类将在追寻未解数学难题的道路上,借助AI的力量,取得更多的突破。
随着AI的发展与完善,在其他科学领域,也许会迎来新的应用与机遇。这些探索或将引领我们踏入一个全新的科学新时代,成为更加智慧的“探索者”。
欢迎大家在下方留言讨论,分享您的看法!
